另一种非线性表数据结构,图(Graph)。和树比起来,这是一种更加复杂的非线性表结构。
组成概念
顶点(vertex)
图中的元素叫作顶点(vertex)。
边(edge)
图中的一个顶点可以与任意其他顶点建立连接关系。这种建立的关系叫作边(edge)。
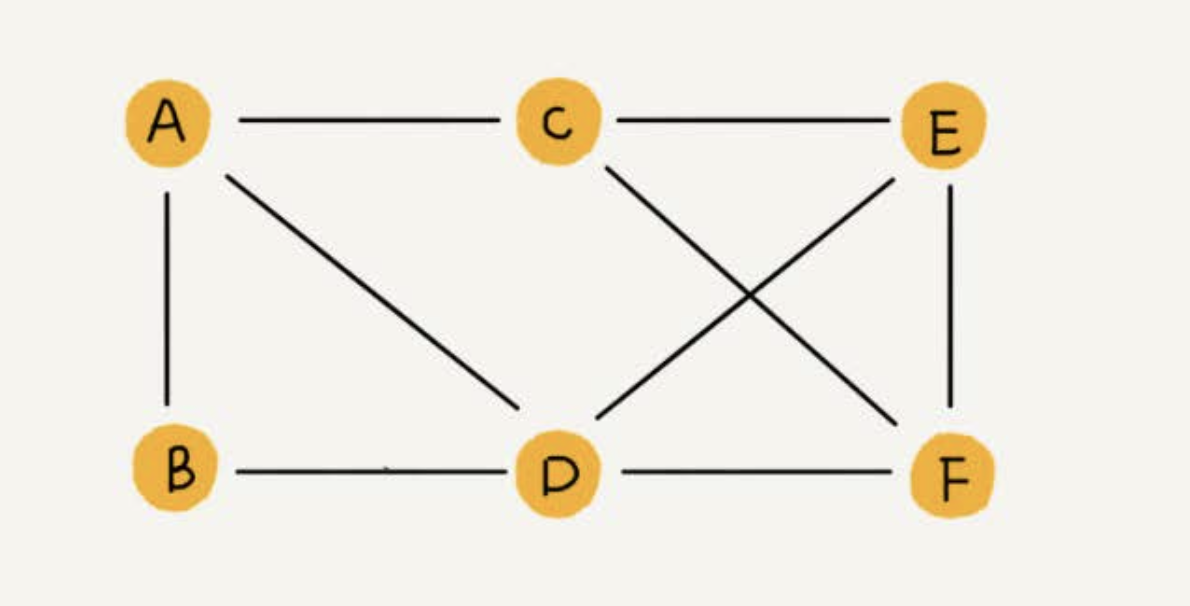
方向
- 边有方向的图叫作“有向图”
- 边没有方向的图就叫作“无向图”
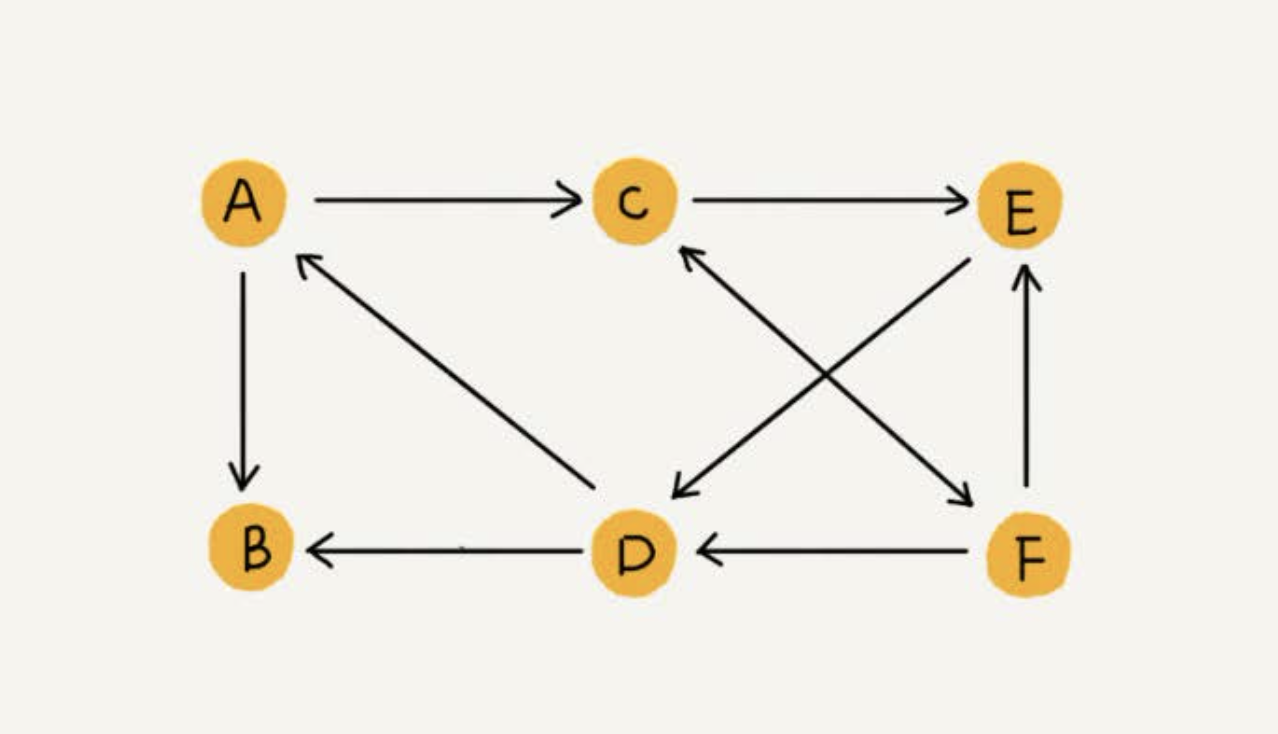
度(degree)
跟顶点相连接的边的条数,叫作顶点的度(degree),
- 无向图中有“度”这个概念,表示一个顶点有多少条边。
- 有向图中,度分为入度(In-degree)和出度(Out-degree)。
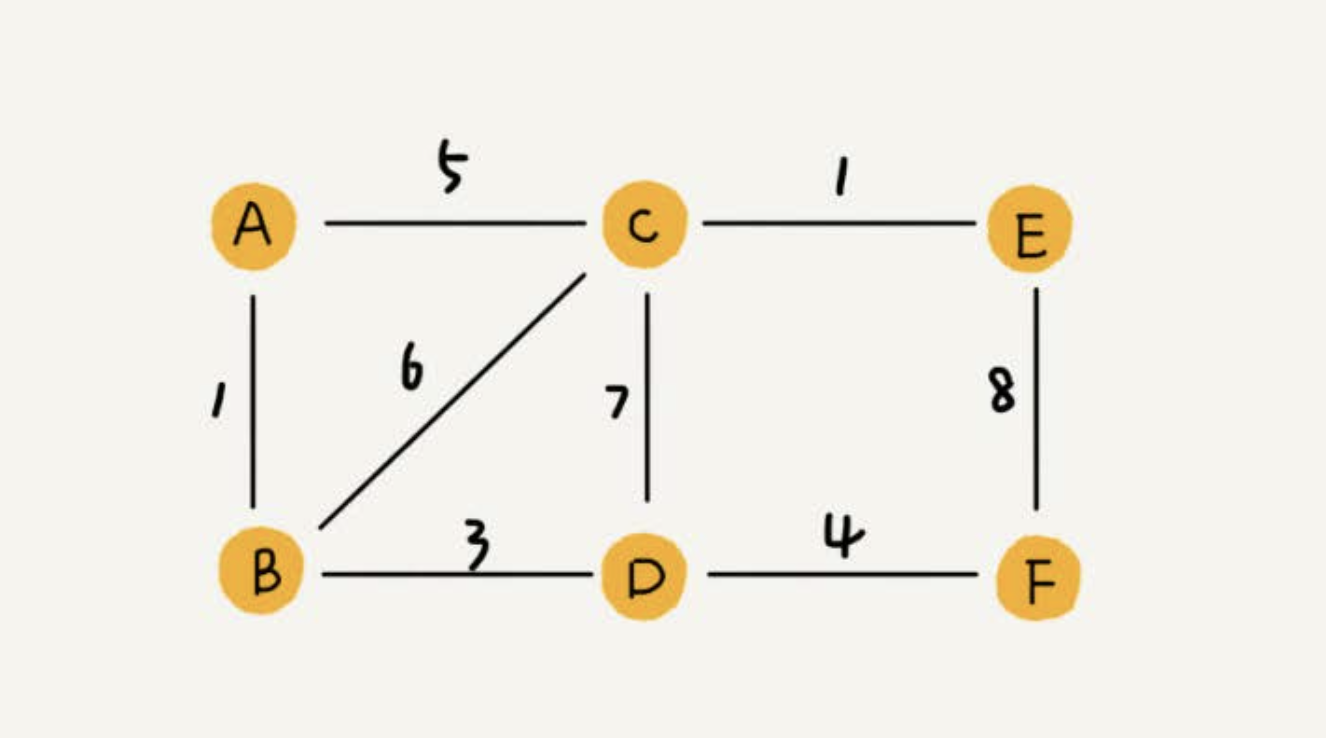
带权图(weighted graph)
在带权图中,每条边都有一个权重(weight)
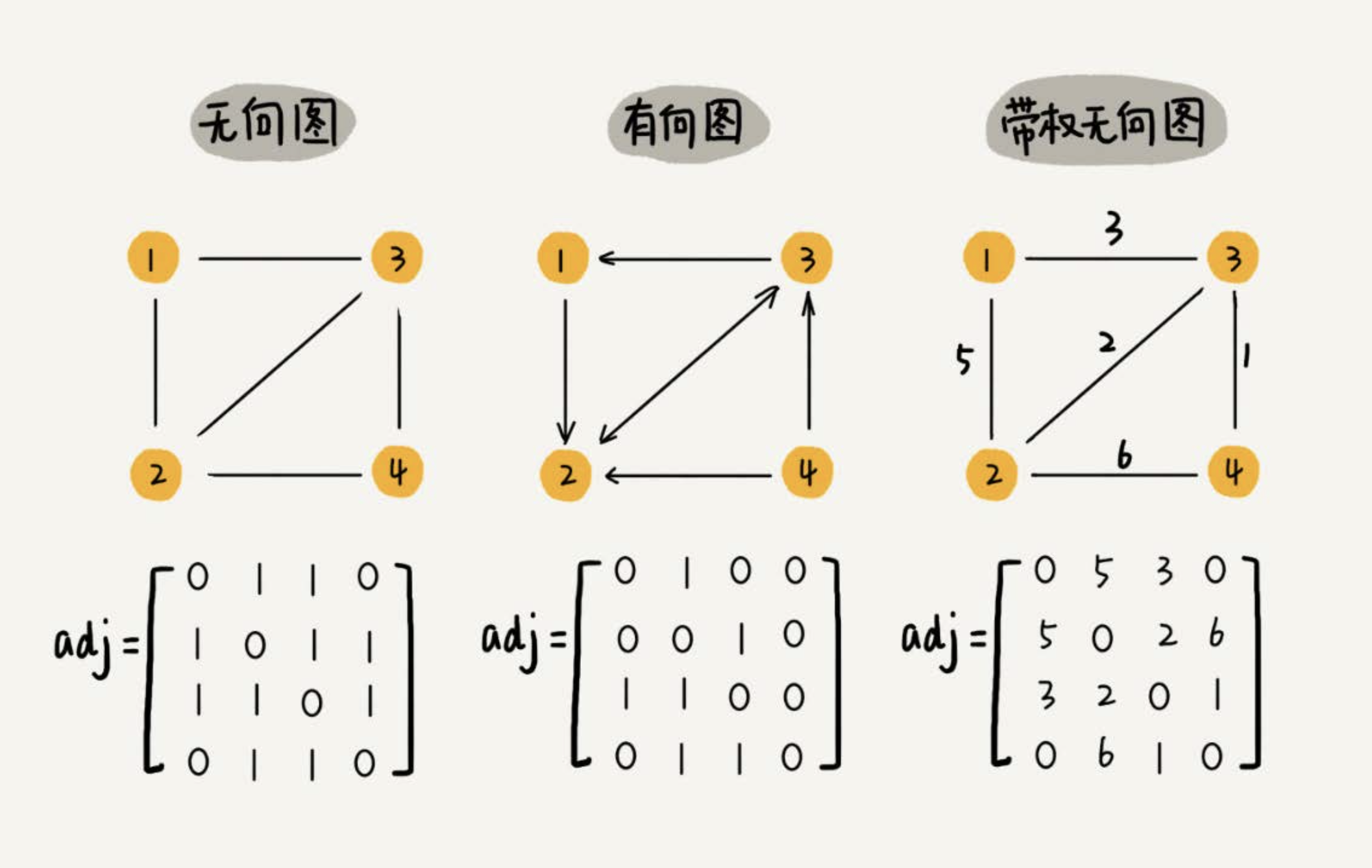
存储方式
邻接矩阵(Adjacency Matrix)
邻接矩阵的底层依赖一个二维数组。
- 对于无向图来说,如果顶点i与顶点j之间有边,我们就将A[i][j]和A[j][i]标记为1;
- 对于有向图来说,如果顶点i到顶点j之间,有一条箭头从顶点i指向顶点j的边,那我们就将A[i][j]标记为1。同理,如果有一条箭头从顶点j指向顶点i的边,我们就将A[j][i]标记为1。
- 对于带权图,数组中就存储 相应的权重。
缺点
可能会造成空间的浪费。
优点
存储方式简单、直接,因为基于数组,所以在获取两个顶点的关系时,就非常高效。
邻接矩阵存储图方便计算。用邻接矩阵的方式存储图,可以将很多图的运算转换成矩阵之间的运算。
比如求解最短路径问题时会提到一个Floyd-Warshall算法,就是利用矩阵循环相乘若干次得到结果。
邻接表(Adjacency List)
每个顶点对应一条链表,链表中存储的是与这个顶点相连接的其他顶点。
图中画的是一个有向图的邻接表存储方式,每个顶点对应的链表里面,存储的是指向的顶点。
对于无向图来说,也是类似的,不过,每个顶点的链表中存储的,是跟这个顶点有边相连的顶点。

如果链过长,为了提高查找效率,可以将链表换成其他更加高效的数据结构,比如红黑树、跳表等。

