堆是一种特殊的二叉树结构,并且可以进行堆排序,堆排序是一种原地的、时间复杂度为O(nlogn)的排序算法。堆常用于实现优先队列。
堆的定义
- 堆是一个完全二叉树;
堆中每一个节点的值都必须大于等于(或小于等于)其子树中每个节点的值。
对于每个节点的值都大于等于子树中每个节点值的堆,叫作“大顶堆”。
- 对于每个节点的值都小于等于子树中每个节点值的堆,叫作“小顶堆”。
数组实现堆
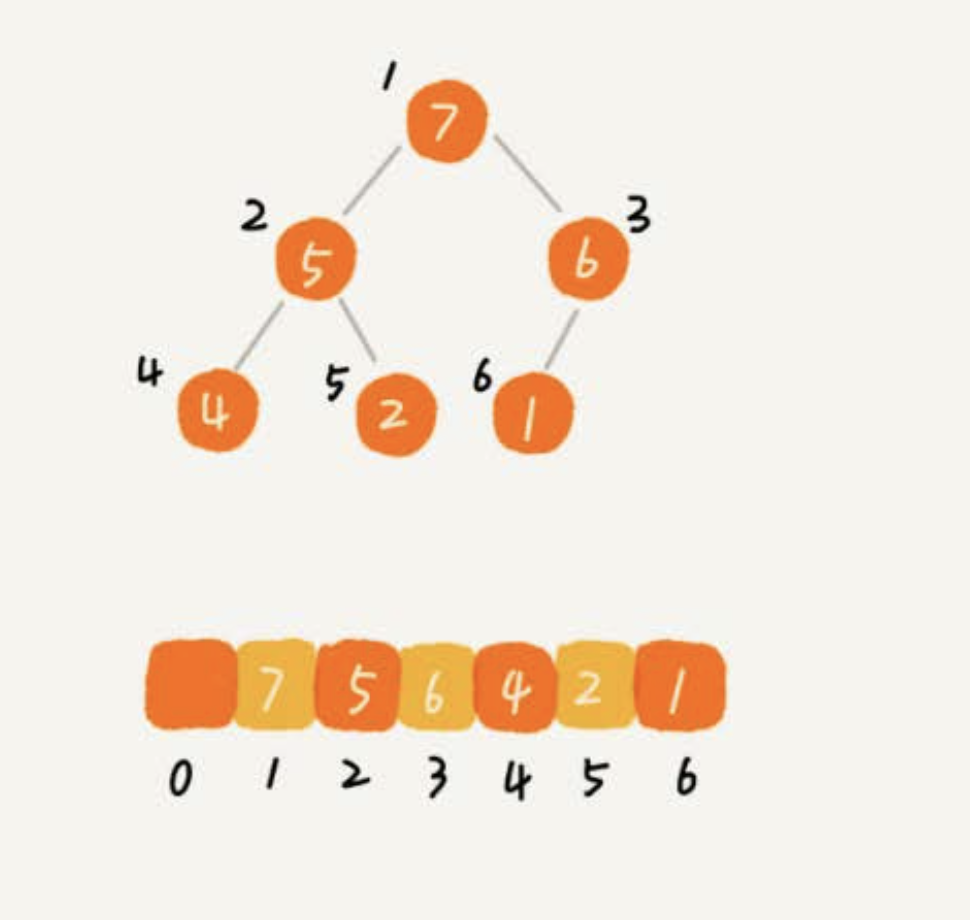
由于堆是一个完全二叉树,所以使用数组实现是最节省空间的。
元素x的位置数组中下标为i,可以得出:
- 左子节点:i * 2
- 右子节点:i * 2 + 1
- 父节点: i / 2
堆化与插入删除
插入元素
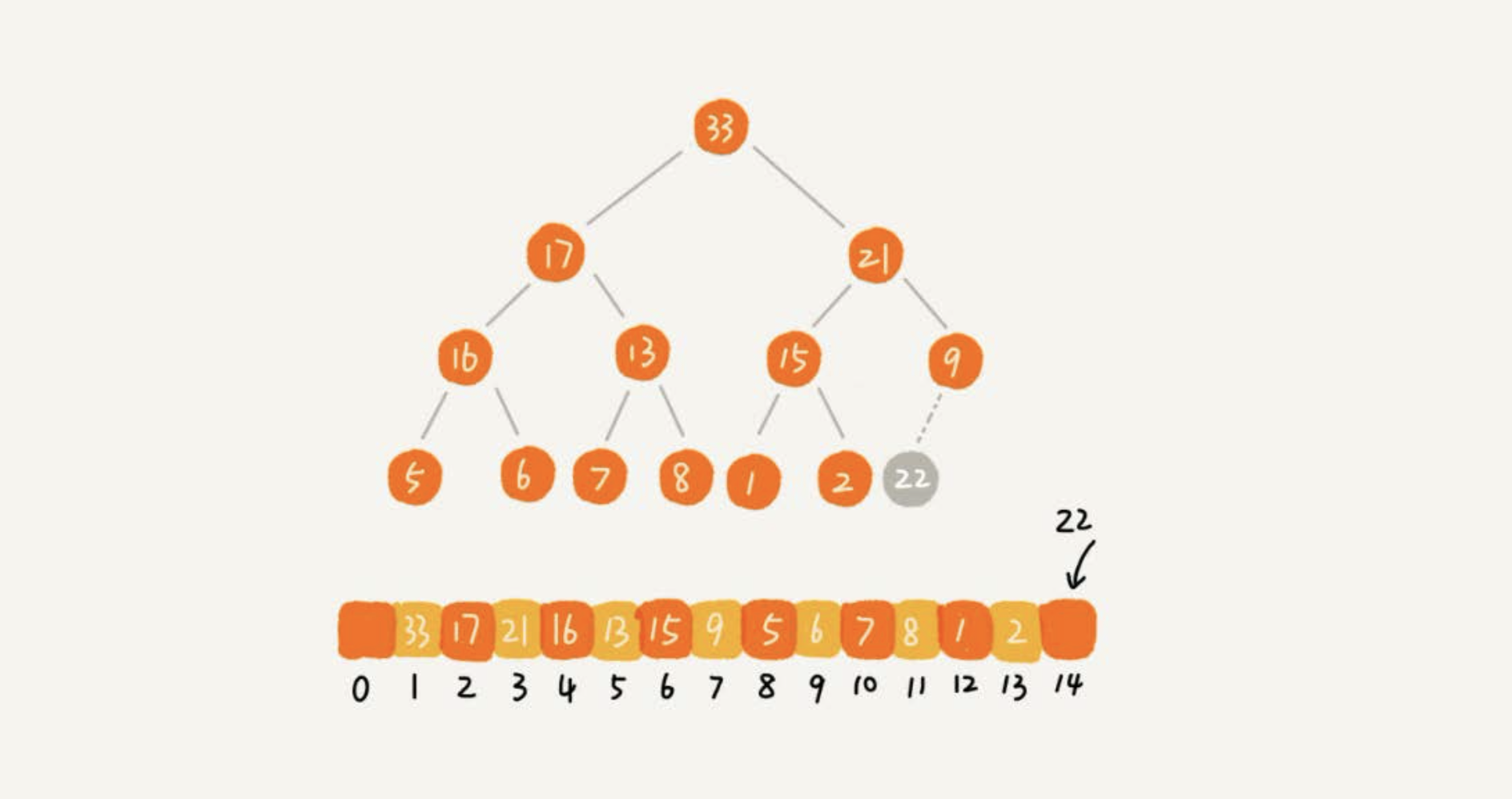
往堆中插入一个元素后,需要继续让其重新满足堆的特性,这个过程就叫作堆化(heapify)。
堆化有两个方式,从下向上(数组最后插入进行调整),从上往下(数组开始插入进行调整)
自底向上堆化
新插入的节点与父节点对比大小。如果不满足子节点小于等于父节点的大小关系,我们就互换两个节点。一直重
复这个过程,直到父子节点之间满足大/小顶堆关系。
删除堆顶元素
即删除最大/最小元素
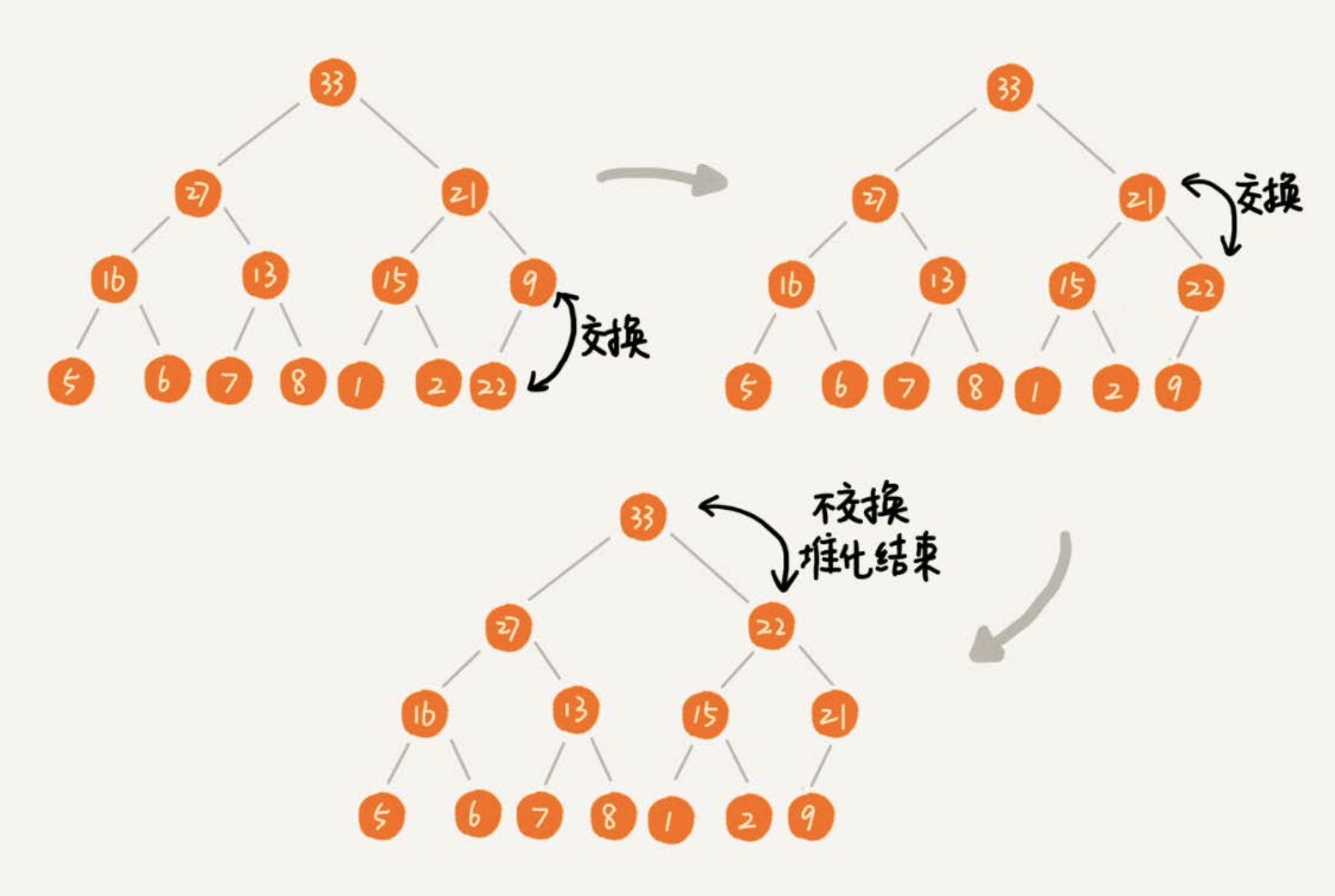
自顶向下堆化
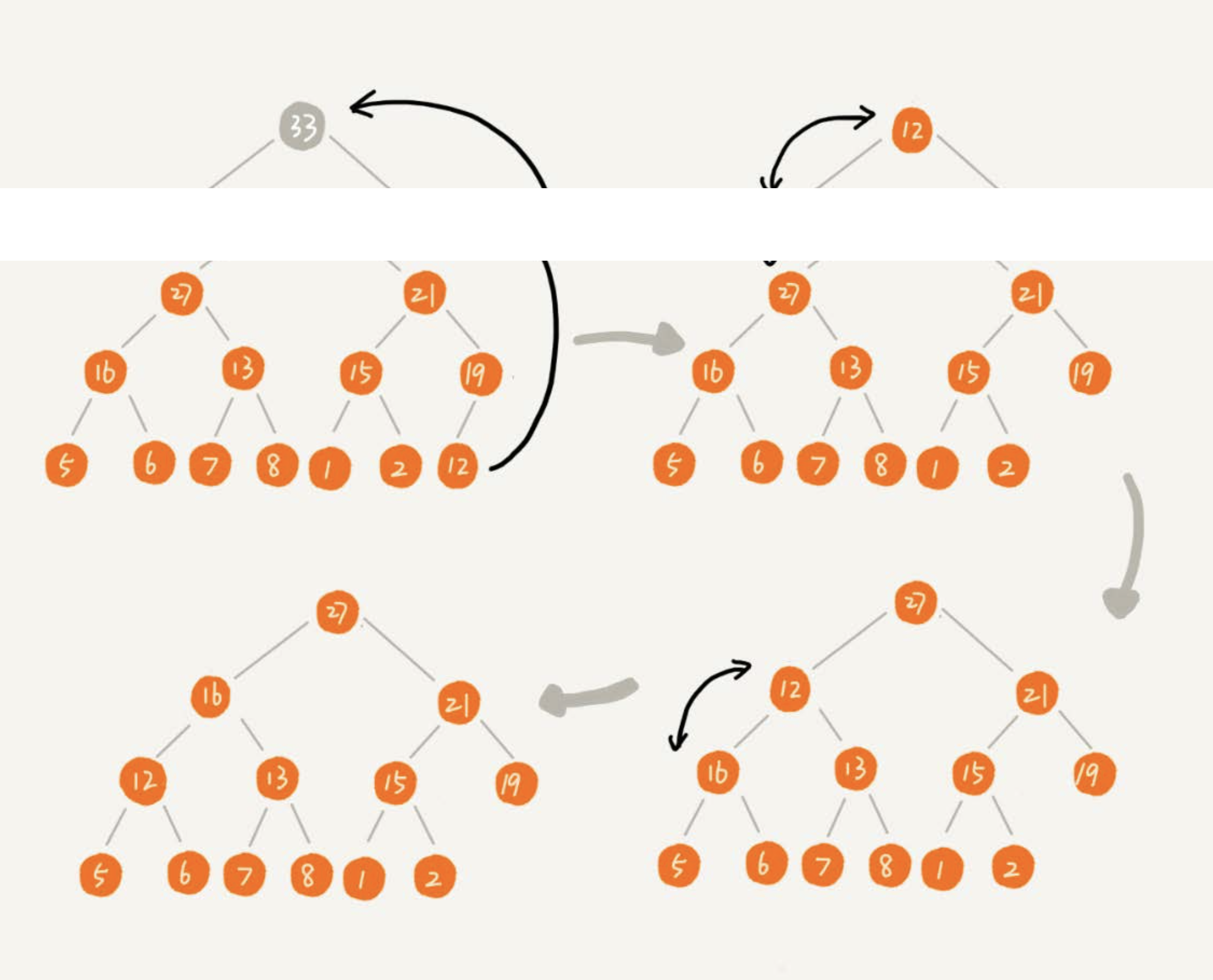
把最后一个节点放到堆顶,然后利用同样的父子节点对比方法。对于不满足父子节点大小关系的,互换两个节点,并且重复进行这个过程,直到父子节点之间满足大小关系为止。这就是从上往下的堆化方法。
因为移除的是数组中的最后一个元素,而在堆化的过程中,都是交换操作,不会出现数组中的“空洞”,所以这种方法堆化之后的结果,肯定满足完全二叉树的特性。
时间复杂度分析
一个包含n个节点的完全二叉树,树的高度不会超过log2n。
堆化的过程是顺着节点所在路径比较交换的,所以堆化的时间复杂度跟树的高度成正比,也就是Ologn)。插入数据和删除堆顶元素的主要逻辑就是堆化,
所以,往堆中插入一个元素和删除堆顶元素的时间复杂度都是O(logn)。
堆排序
包含两个步骤
建堆
- 从前往后处理数组,并且每个数据都是从下往上堆化。
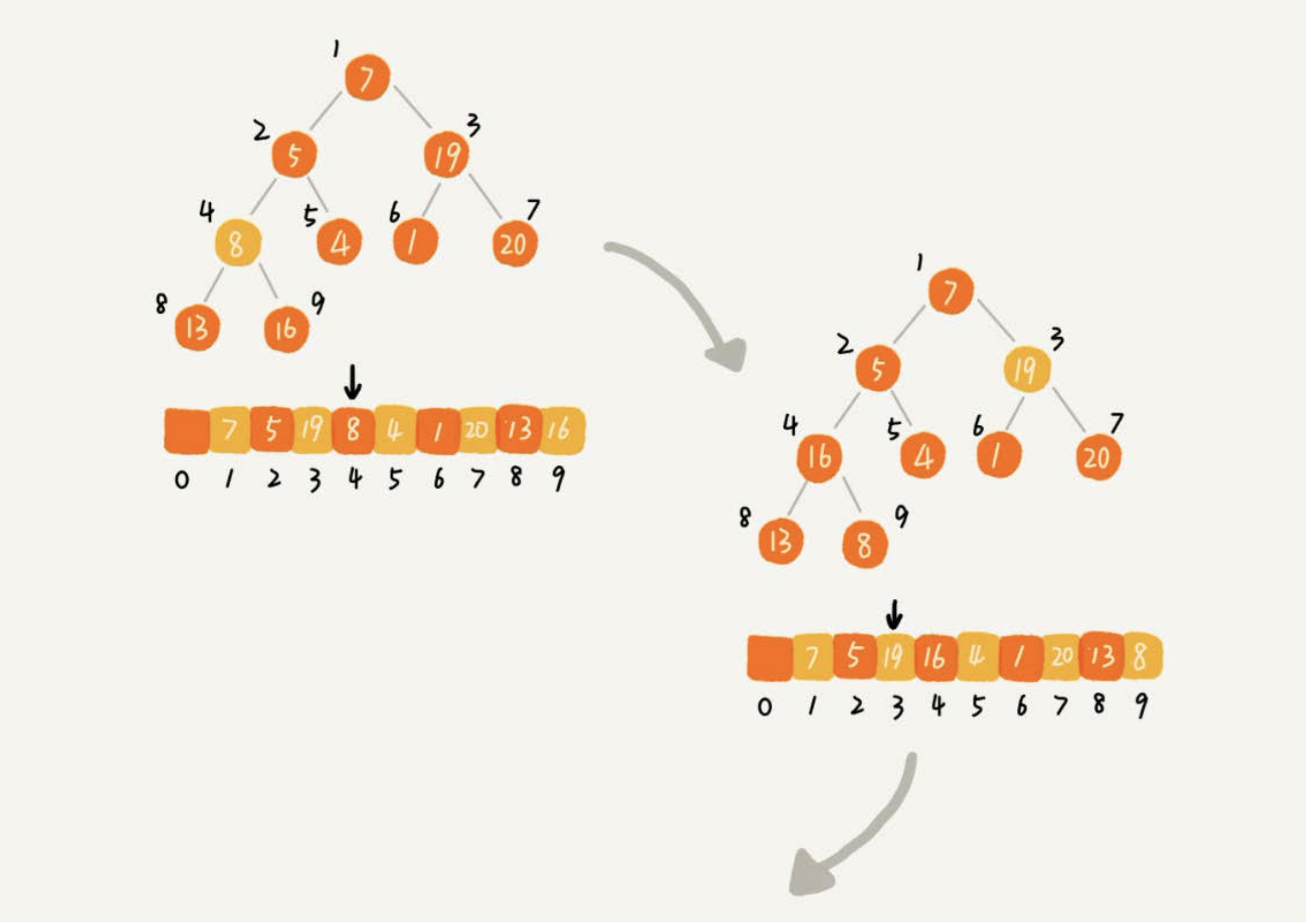
从后往前处理数组,并且每个数据都是从上往下堆化。
下标从n/2开始到1的数据进行堆化
- 下标是n/2+到n的节点是叶子节点,不需要堆化
排序
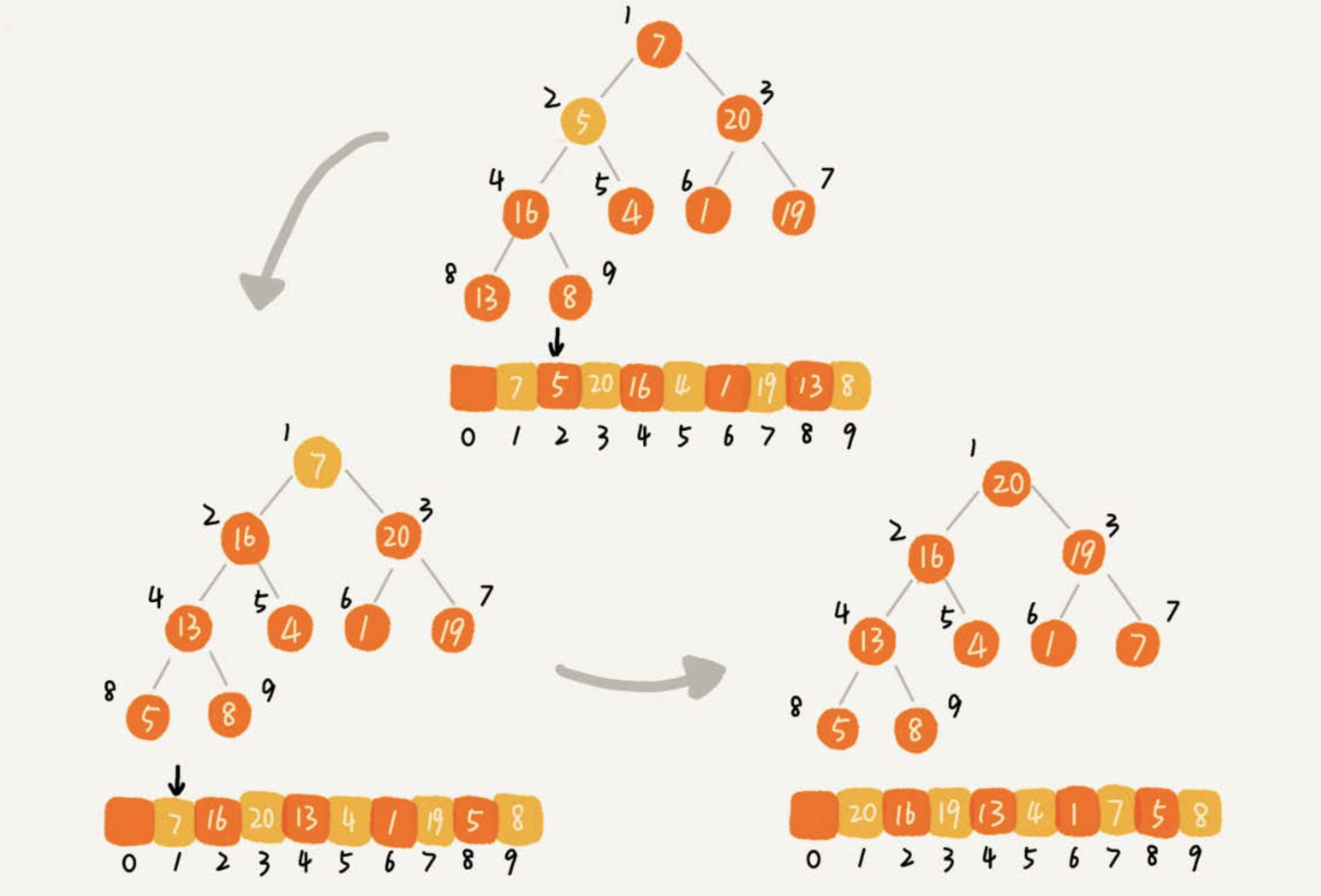
建堆结束之后,数组中的数据已经是按照大/小顶堆的特性来组织的。数组中的第一个元素就是堆顶,也就是最大/小的元素。
- 把堆顶元素跟最后一个元素交换,那最大元素就放到了下标为n的位置。当堆顶元素移除之后,把下标为n的元素放到堆顶
- 通过堆化的方法,将剩下的n-1个元素重新构建成堆
- 堆化完成之后,我们再取堆顶的元素,放到下标是n-1的位置,
一直重复这个过程,直到最后堆中只剩下标为1的一个元素,排序工作就完成了。
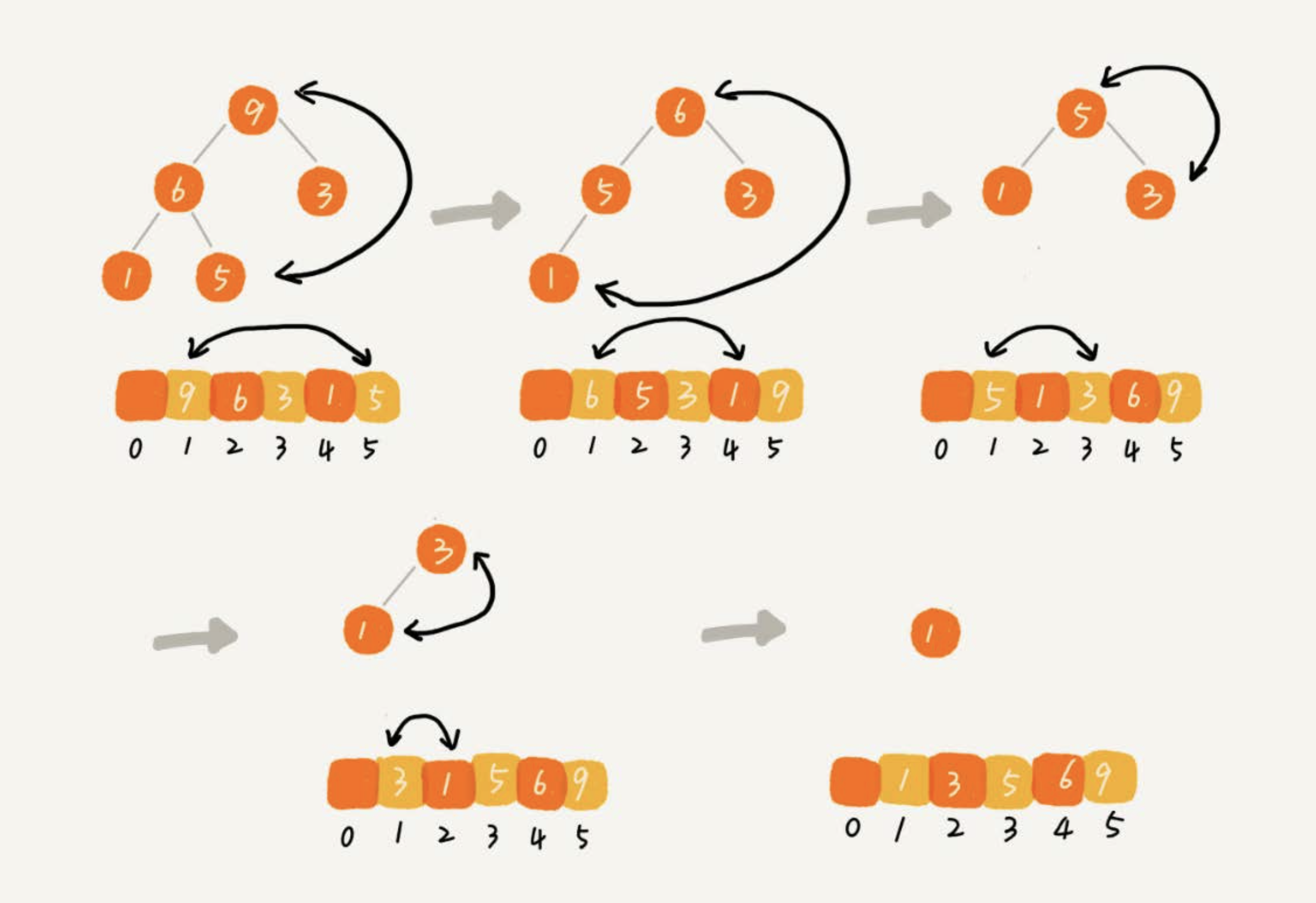
复杂度分析
整个堆排序的过程,都只需要极个别临时存储空间,所以堆排序是原地排序算法。
堆排序包括建堆和排序两个操作,所以,堆排序整体的时间复杂度是O(nlogn)。
- 建堆过程的时间复杂度是O(n)
- 排序过程的时间复杂度是O(nlogn)
堆排序不是稳定的排序算法,因为在排序的过程,存在将堆的最后一个节点跟堆顶节点互换的操作,所以就有可能改变值相同数据的原始相对顺序。
为什么快速排序要比堆排序性能好?
堆排序数据访问的方式没有快速排序友好
对于快速排序来说,数据是顺序访问的。而对于堆排序来说,数据是跳着访问的。而不是像快速排序那样,局部顺序访问,所以,这样对CPU缓存是不友好的。
对于同样的数据,在排序过程中,堆排序算法的数据交换次数要多于快速排序
排序提过两个概念,有序度和逆序度。
对于基于比较的排序算法来说,整个排序过程就是由两个基本的操作组成的,比较和交换(或移动)。
快速排序数据交换的次数不会比逆序度多。
但是堆排序的第一步是建堆,建堆的过程会打乱数据原有的相对先后顺序,导致原数据的有序度降低。
比如,对于一组已经有序的数据来说,经过建堆之后,数据反而变得更无序了。

