二叉查找树。二叉查找树是最常用的一种二叉树,理想情况下,各类操作的时间复杂度是O(logn)。不过,二叉查找树在频繁的动态更新过程中,可能会出现树的高度远大于log2n的情况,从而导致各个操作的效率下降。极端情况下,二叉树会退化为链表,时间复杂度会退化到O(n)。
平衡二叉查找树
平衡二叉树的定义是:二叉树中任意一个节点的左右子树的高度相差不能大于1。
平衡二叉查找树不仅满足上面平衡二叉树的定义,还满足二叉查找树的特点。最先被发明的平衡二叉查找树是AVL树,它严格符合我刚讲到的平衡二叉查找树的定义,即任何节点的左右子树高度相差不超过1,是一种高度平衡的二叉查找树。
但是很多平衡二叉查找树其实并没有严格符合上面的定义(树中任意一个节点的左右子树的高度相差不能大于1),比如红黑树,它从根节点到各个叶子节点的最长路径,有可能会比最短路径大一倍。
- 发明平衡二叉查找树这类数据结构的初衷是,解决普通二叉查找树在频繁的插入、删除等动态更新的情况下,出现时间复杂度退化的问题。
种类
平衡二叉查找树其实有很多,比如,Splay Tree(伸展树)、Treap(树堆)等,但是提到平衡二叉查找树,最常听到都是红黑树。
红黑树 Red-Black Tree
R-B Tree。它是一种不严格的平衡二叉查找树。
要求如下:
- 根节点是黑色的;
- 每个叶子节点都是黑色的空节点(NIL),也就是说,叶子节点不存储数据;(主要是为了简化红黑树的代码实现而设置,实际中所有叶子结点都指向同一个空黑节点)
- 任何相邻的节点都不能同时为红色,也就是说,红色节点是被黑色节点隔开的;
- 每个节点,从该节点到达其可达叶子节点的所有路径,都包含相同数目的黑色节点;
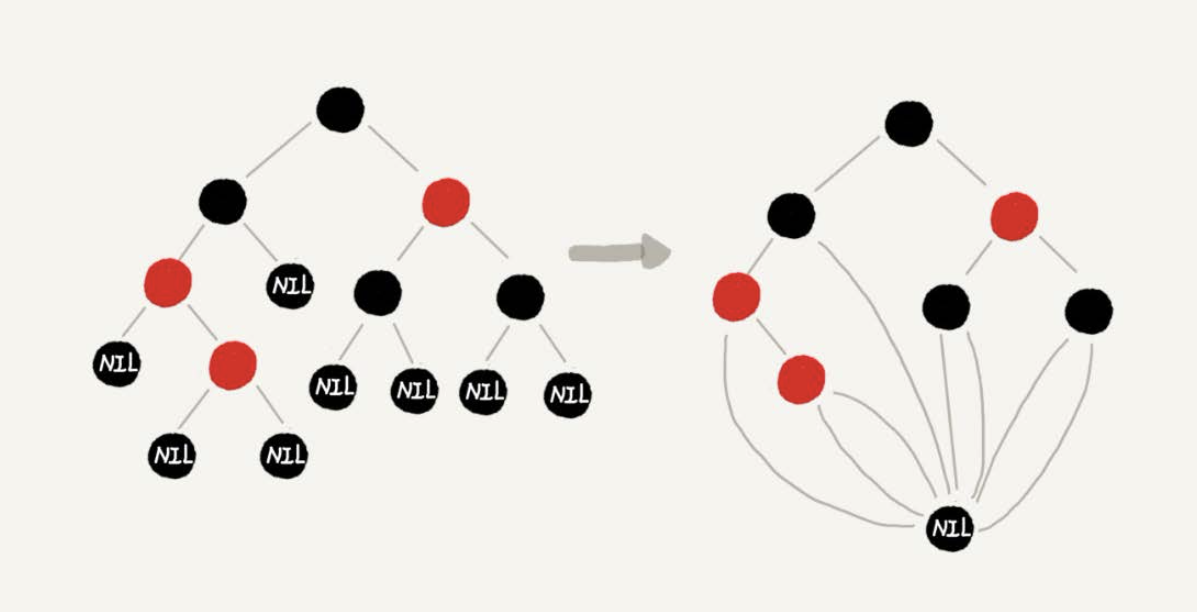
黑色空叶子节点
红黑树添加黑色的空的叶子节点,不会浪费存储空间。虽然在讲解或者画图的时候,每个黑色的、空的叶子节点都是独立画出来的。实际上,在具体实现的时候,只需要像下面这样,共用一个黑色的、空的叶子节点就行了。
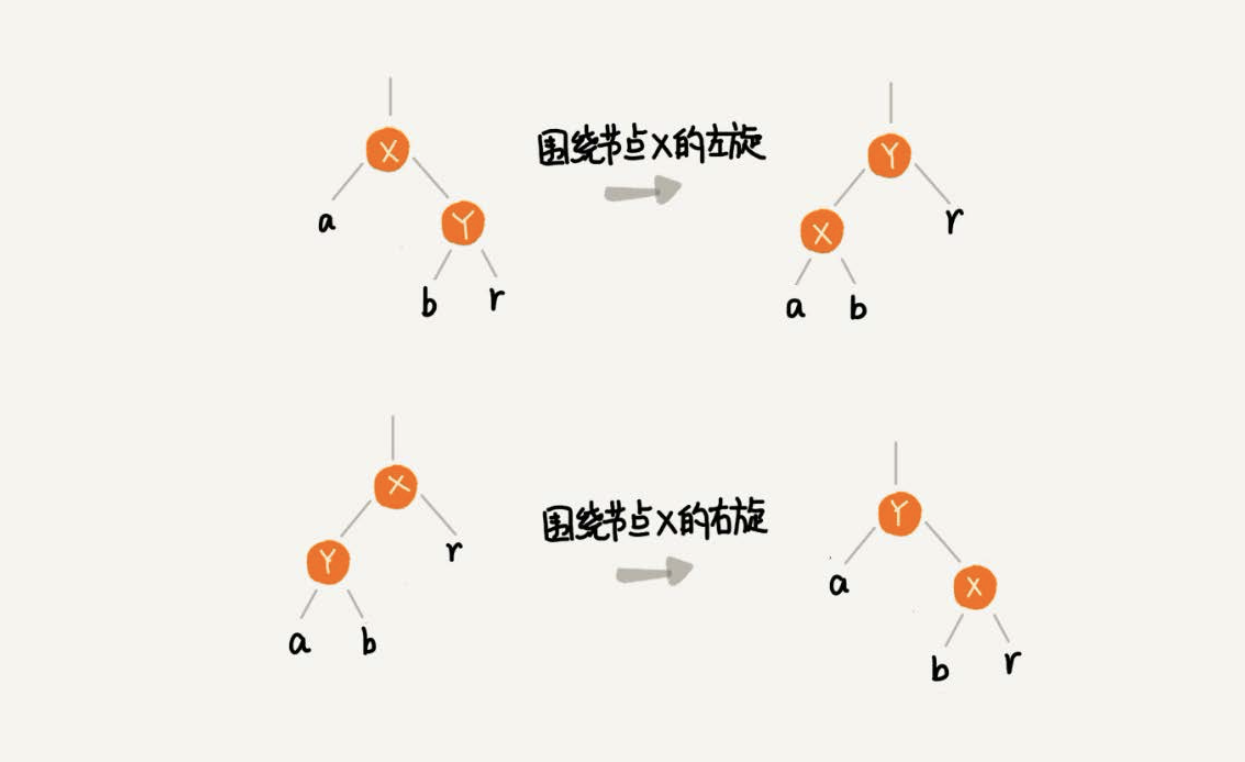
左旋(rotate left)、右旋(rotate right)
关注节点
红黑树的平衡调整过程是一个迭代的过程。我们把正在处理的节点叫作关注节点。关注节点会随着不停地迭代处理,而不断发生变化。

