二叉查找树(Binary Search Tree)
二叉查找树要求,在树中的任意一个节点,其左子树中的每个节点的值,都要小于这个节点的值,而右子树节点的值都大 于这个节点的值。
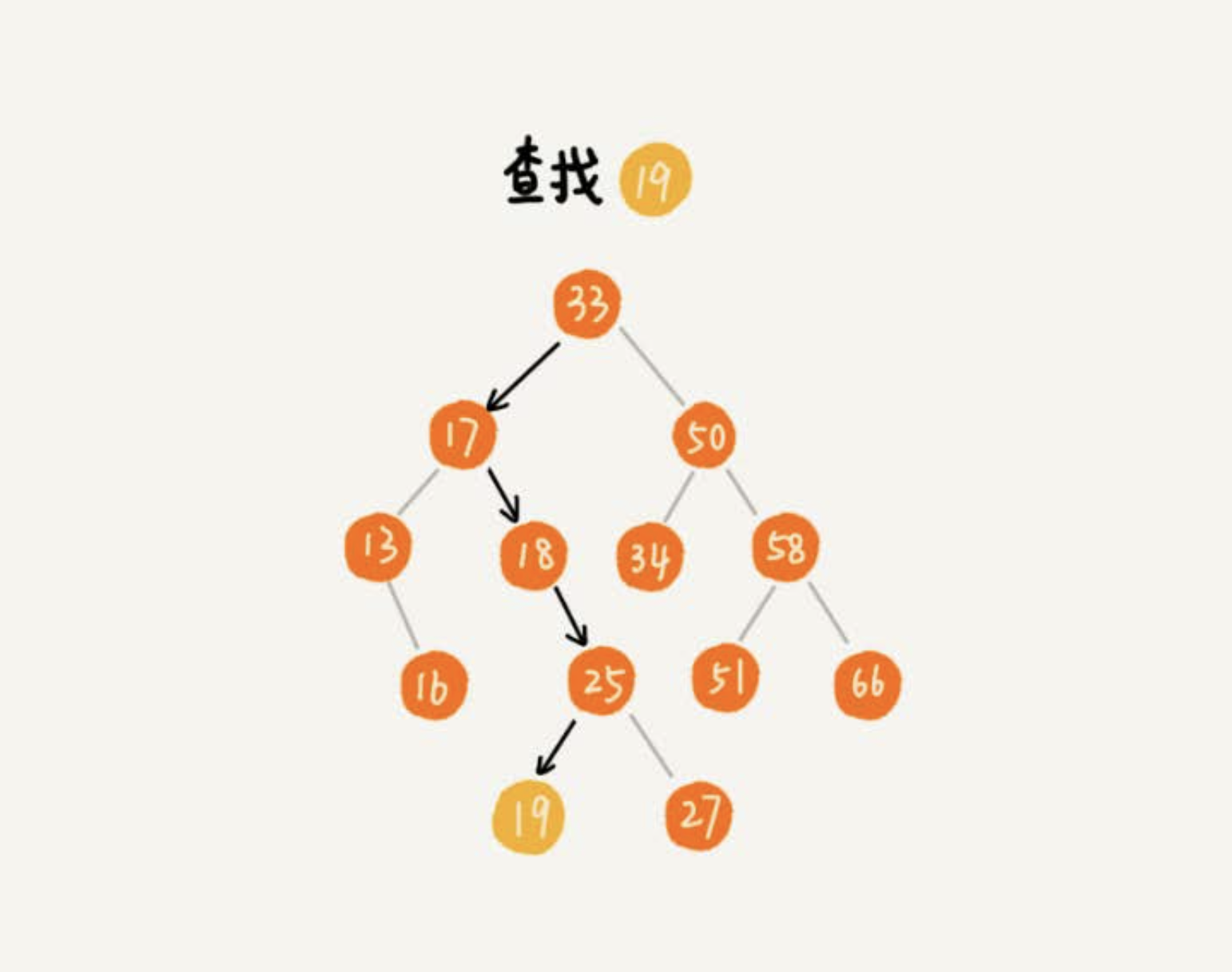
查询
- 从根节点出发,如果它等于我们要查找的数据,那就返回
- 如果要查找的数据比根节点的值小,那就在左子树中递归查找
- 如果要查找的数据比根节点的值大,那就在右子树中递归查找
中序遍历即可得到有序数据
示例
1 | BinarySearchTreeNode find(int data) { |
插入
二叉查找树的插入过程有点类似查找操作。新插入的数据一般都是在叶子节点上,所以只需要从根节点开始,依次比较要插入的数据和节点的大小关系。
- 如果要插入的数据比节点的数据大,并且节点的右子树为空,就将新数据直接插到右子节点的位置;
如果不为空,就再递归遍历右子树,查找插入位置。
如果要插入的数据比节点数值小,并且节点的左子树为空,就将新数据插入到左子节点的位置;
- 如果不为空,就再递归遍历左子树,查找插入位置。
示例
1 | void insert(int data) { |
删除
删除的情况比较复杂,主要有三种情况:
- 如果要删除的节点没有子节点,只需要直接将父节点中,指向要删除节点的指针置为null。比如图中的删除节点55。
- 如果要删除的节点只有一个子节点(只有左子节点或者右子节点),只需要更新父节点中,指向要删除节点的指针,让它指向要删除节点的 子节点就可以了。比如图中的删除节点13。
- 如果要删除的节点有两个子节点,这就比较复杂了。需要找到这个节点的右子树中的最小节点,把它替换到要删除的节点上。然后再删除掉这个最小节点,因为最小节点肯定没有左子节点(如果有左子结点,那就不是最小节点了),所以,可以应用上面两条规则来删除这个最小节点。比如图中的删除节点18。
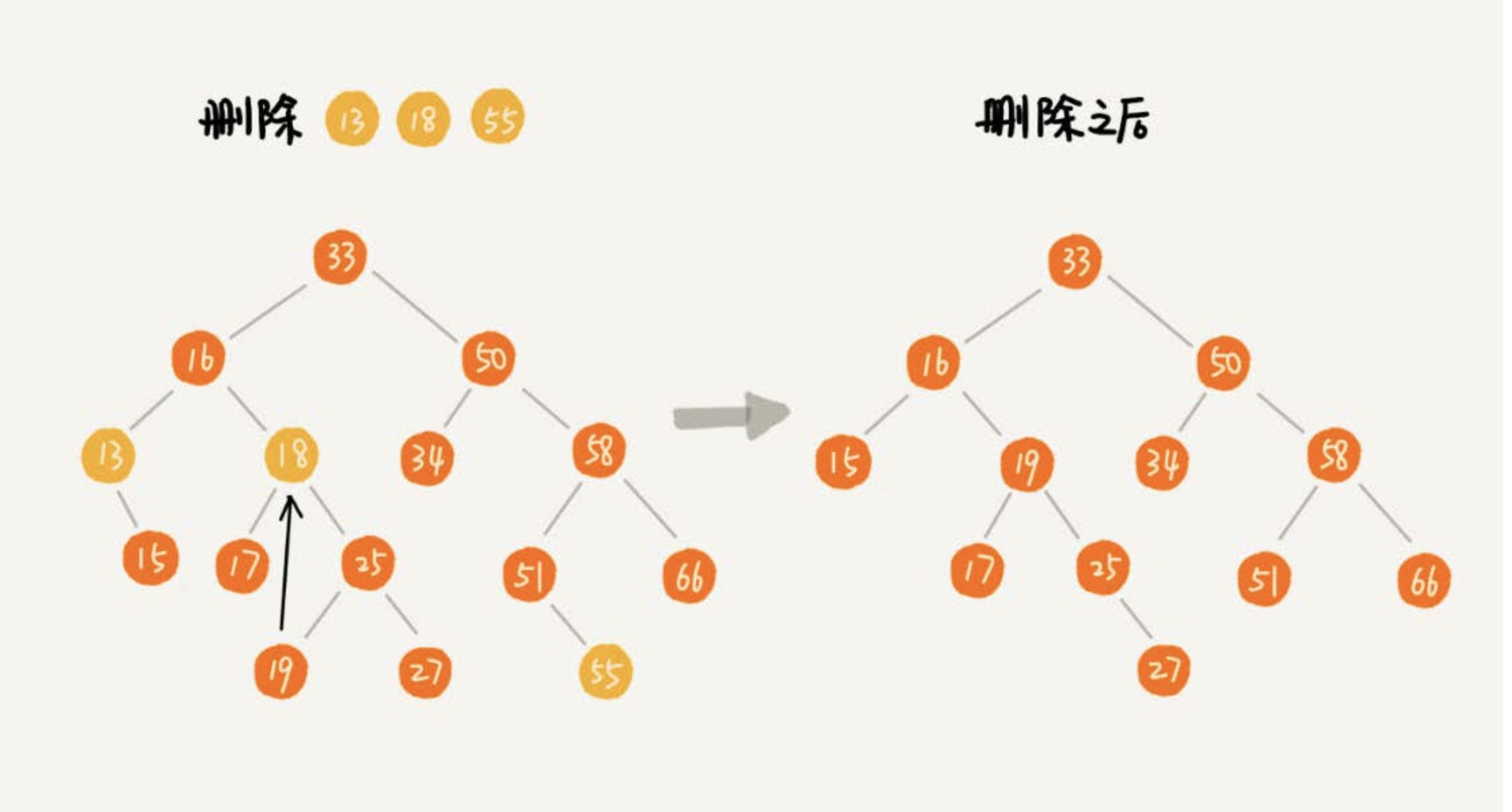
示例
1 | void remove(int data) { |
实际上,关于二叉查找树的删除操作,还有个非常简单、取巧的方法,就是单纯将要删除的节点标记为“已删除”,但是并不真正从树中将这个节点去掉。原本删除的节点还需要存储在内存中,比较浪费内存空间,但是删除操作就变得简单了很多。而且,这种处理方法也并没有增加插入、查找操作代码实现的难度。
有序数组构建平衡二叉树
1 | BinarySearchTree sortedArrayToBST(int[] nums) { |
支持重复数据的二叉查找树
- 每个节可保存多个相同数据,通过链表或者支持动态扩容的数据等结构
- 相同节点的值存在时,将其插入到右边,即当作大于进行处理。
- 查找数据时,不停止查找而是继续在右子树查找,直到遇到叶子结点才停止
- 删除时候也要从下向上依次删除
时间复杂度
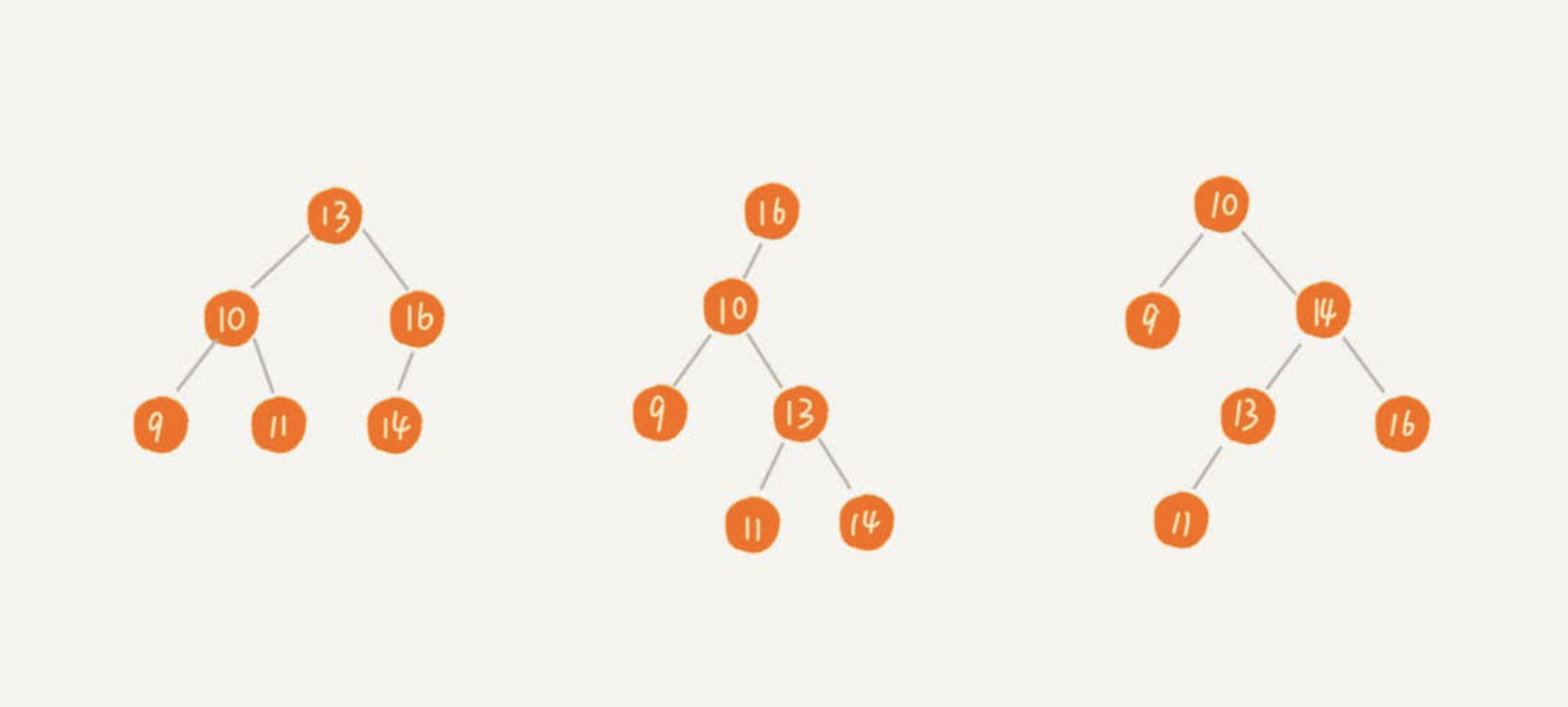
对于同一组数据,构造了三种二叉查找树。它们的查找、插入、删除操作的执行效率都是不一样的。
图中第一种二叉查找树,根节点的左右子树极度不平衡,已经退化成了链表,所以查找的时间复杂度就变成了O(n)。

树的高度
不管操作是插入、删除还是查找,时间复杂度其实都跟树的高度成正比,也就是O(height)。
树的高度就等于最大层数减一,为了方便计算,我们转换成层来表示。从图中可以看出,包含n个节点的完全二叉树中,第一层包含1个节点,第二层包含2个节点,第三层包含4个节点,依次类推,下面一层节点个数是上一层的2倍,第K层包含的节点个数就是2^(K-1)。
在二叉查找树中,查找、插入、删除等很多操作的时间复杂度都跟树的高度成正比。两个极端情况的时间复杂度分别是O(n)和O(logn),分别对应二叉树退化成链表的情况和完全二叉树。
- 极不平衡的状态下,退化为链表,插入、删除、查询操作的时间复杂度为O(n)
- 平衡二叉树的高度接近logn, 所以插入、删除、查询操作的时间复杂度比较稳定,是O(logn)

