之前记录的都是线性表结构,栈、队列等,而树这种结构比线性表结构复杂的多,本文主要记录了树的基础知识。
树的种类
- 树、二叉树
- 二叉查找树
- 平衡二叉查找树
- 红黑树
- 递归树
相关概念
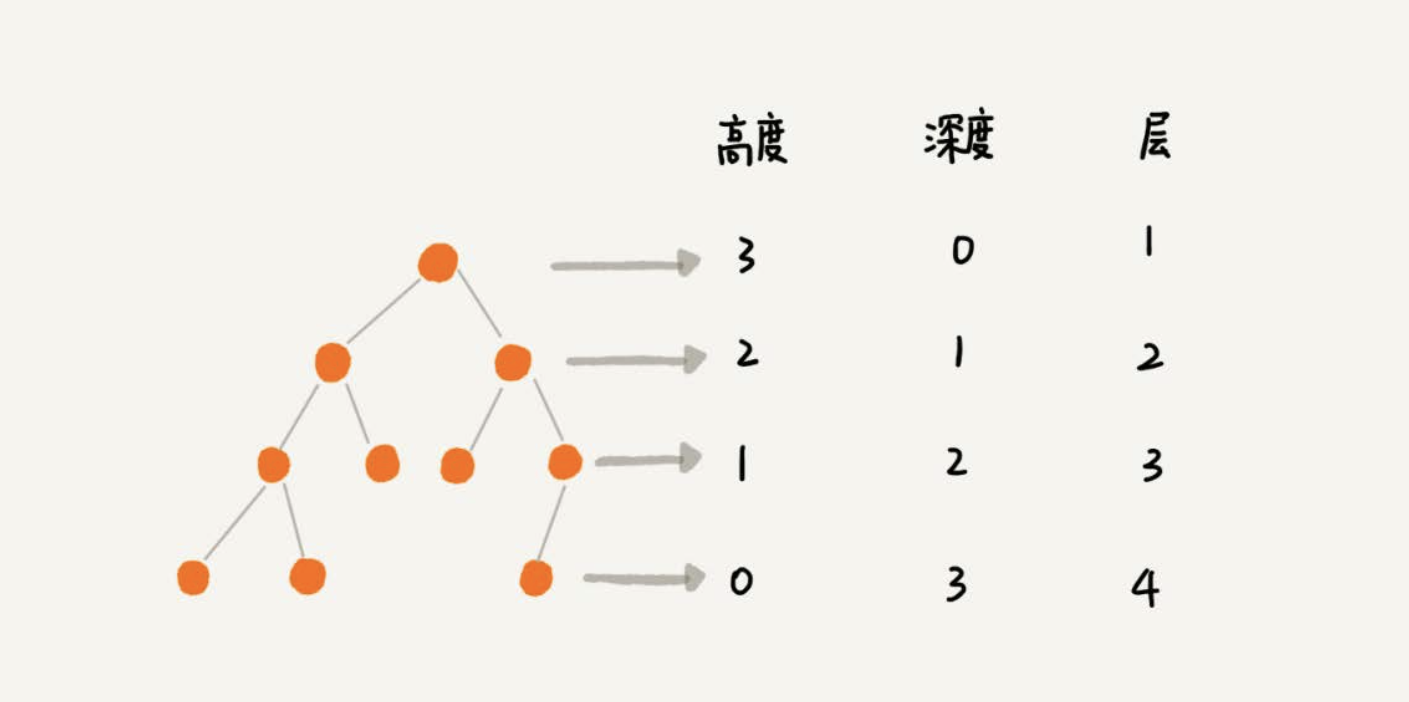
关于“树”的三个比较相似的概念:高度(Height)、深度(Depth)、层(Level)。它们的定义是这样的:
- 节点的高度:节点到叶子结点的最长路径(边数),从下往上数
- 节点的深度:根节点到这个节点所经历的边的个数,从上往下数
- 节点的层数:节点的深度+1
- 树的高度: 根节点的高度
二叉树 Binary Tree
满二叉树
叶子节点全都在最底层,除了叶子节点之外,每个节点都有左右两个子节点,这种二叉树就叫作满二叉树。
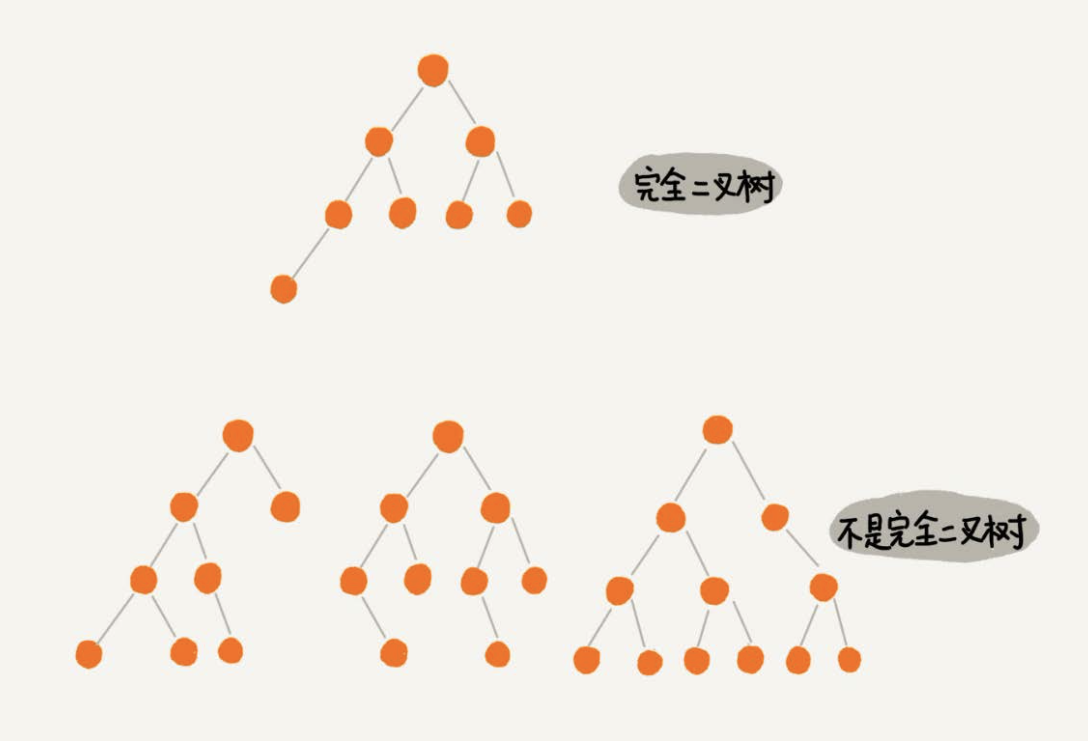
完全二叉树
叶子节点都在最底下两层,最后一层的叶子节点都靠左排列,并且除了最后一层,其他层的节点个数都要达到最大,这种二叉树叫作完全二叉树
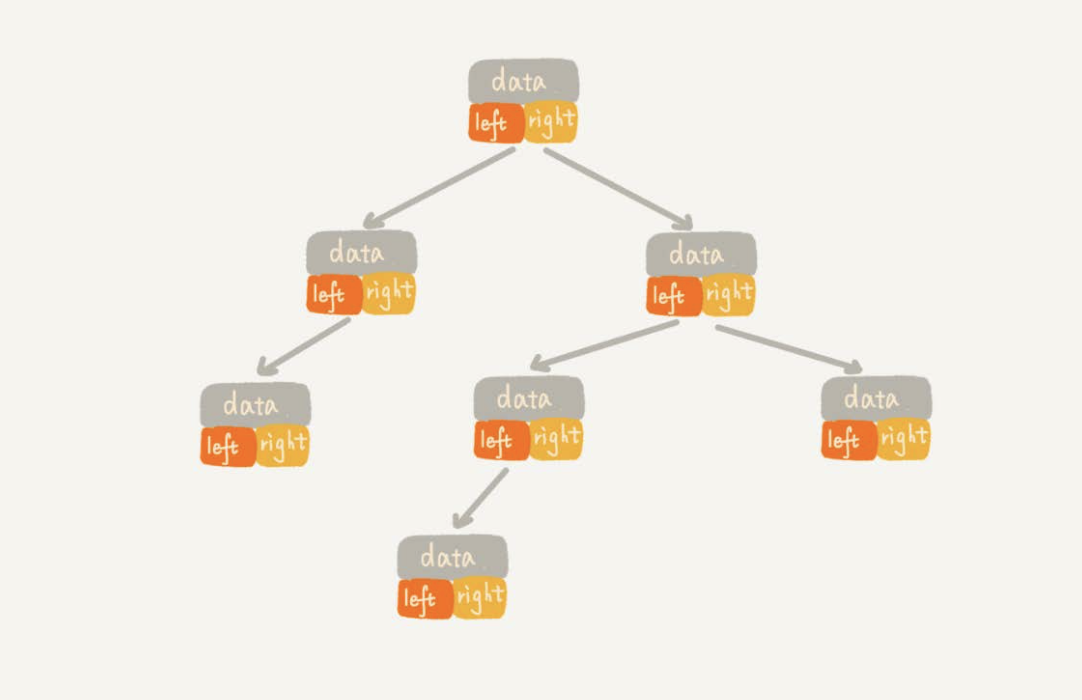
通过指针存储二叉树 链式二叉树
类似于链表一样,通过指针表示叶子结点。
通过数组存储二叉树
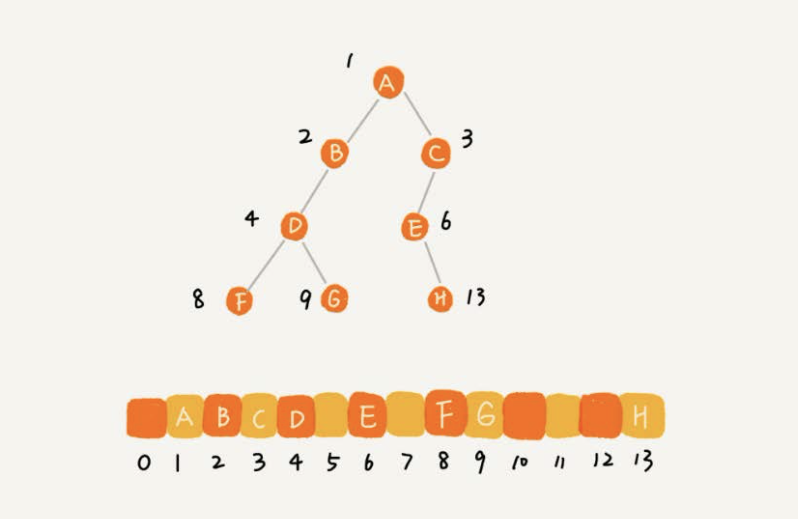
数组顺序存储的方式比较适合完全二叉树
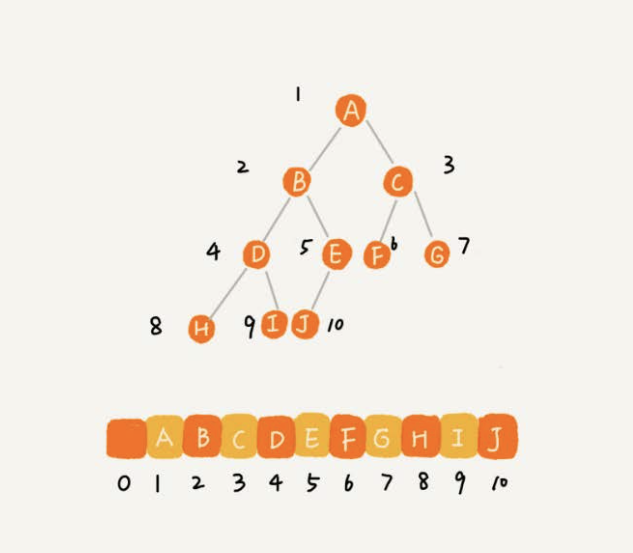
基于数组的顺序存储法。把根节点存储在下标i = 1的位置,那左子节点存储在下标2 i = 2的位置,右子节点存储在2 i + 1 = 3的位置。以此类 推,B节点的左子节点存储在2 i = 2 2 = 4的位置,右子节点存储在2 i + 1 = 2 2 + 1 = 5的位置。
节点X存储在数组中下标为i的位置,
- 下标为2 * i 的位置存储的就是左子节点,
- 下标为2 * i + 1的位置存储的就是右子节点
- 下标为i / 2的位置存储就是它的父节点
一般情况下,为了方便计算子节点,根节点会存储在下标为1的位置。
非完全二叉树,其实会浪费比较多的数组存储空间
二叉树的遍历
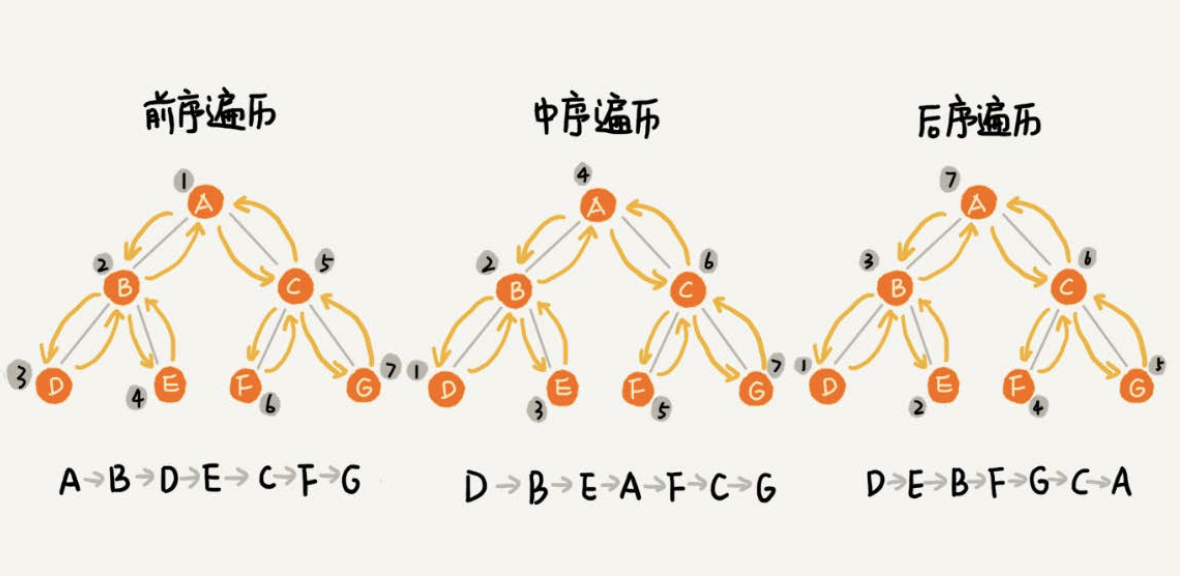
树的遍历常见的方法有三种,前序遍历、中序遍历和后序遍历。其中,前、中、后序,表示的是节点与它的左右子树节点遍历打印的先后顺序。
- 前序遍历是指,对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。
- 中序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。
- 后序遍历是指,对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
递归公式
- 前序遍历的递推公式: preOrder(r) = print r->preOrder(r->left)->preOrder(r->right)
- 中序遍历的递推公式: inOrder(r) = inOrder(r->left)->print r->inOrder(r->right)
- 后序遍历的递推公式: postOrder(r) = postOrder(r->left)->postOrder(r->right)->print r
按层遍历
JAVA实现的简单的示例
1 | public class BinaryTree { |

