桶排序
计数排序
计数排序只能用在数据范围不大的场景中,如果数据范围k比要排序的数据n大很多,就不适合用计数排序了。
而且,计数排序只能给非负整数排序,如果要排序的数据是其他类型的,要将其在不改变相对大小的情况下,转化为非负整数。
- 如果存在负数,则先将全部数据增加最小值的绝对值,转化为正整数,最后再加最小值。
- 如果存在小数,则现将全部数据乘以小数位数,转化为整数,最后除以小数位数。
示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55public static void countingSort(int[] nums) {
if (nums == null || nums.length <= 1) {
return;
}
// 解决负数
int min = 0;
for (int i = 1; i < nums.length; i++) {
if (min > nums[i]) {
min = nums[i];
}
}
if (min < 0) {
for (int i = 0; i < nums.length; i++) {
nums[i] = nums[i] + Math.abs(min);
}
}
// 解决小数 略...
// 查找数组中数据的范围
int max = nums[0];
for (int i = 1; i < nums.length; i++) {
if (max < nums[i]) {
max = nums[i];
}
}
// 创建计数数组
int[] counter = new int[max + 1];
for (int i = 0; i < counter.length; i++) {
counter[i] = 0;
}
// 计算每个元素的个数,放入计数数组中
for (int i = 0; i < nums.length; i++) {
counter[nums[i]]++;
}
// 依次累加
for (int i = 1; i <= max; i++) {
counter[i] = counter[i - 1] + counter[i];
}
// 创建临时数组,存储排序之后的结果
int[] temp = new int[nums.length];
// 计算排序步骤,从后向前遍历
for (int i = nums.length - 1; i >= 0; i--) {
int index = counter[nums[i]] - 1;
temp[index] = nums[i];
counter[nums[i]]--;
}
// 复制临时数组到原数组
for (int i = 0; i < nums.length; i++) {
int t = temp[i];
if (min < 0) {
t = t + min;
}
nums[i] = t;
}
}
基数排序
假设有10万个手机号码,将这10万个手机号码从小到大排序。
这个问题里有这样的规律:假设要比较两个手机号码a,b的大小,如果在前面几位中,a手机号码已经比b手机号码大了,那后面的几位就不用看了。 借助稳定排序算法,这里有一个巧妙的实现思路。先按照最后一位来排序手机号码,然后,再按照倒数第二位重新排序,以此类推,最后按照第一位重新排序。经过11次排序之后,手机号码就都有序了。
注意,这里按照每位来排序的排序算法要是稳定的,否则这个实现思路就是不正确的。因为如果是非稳定排序算法,那最后一次排序只会考虑最高位的大小顺序,完全不管其他位的大小关系,那么低位的排序就完全没有意义了。
根据每一位来排序,可以用桶排序或者计数排序,它们的时间复杂度可以做到O(n)。如果要排序的数据有k位,那我们就需要k次桶排序或者计数排 序,总的时间复杂度是O(k*n)。当k不大的时候,比如手机号码排序的例子,k最大就是11,所以基数排序的时间复杂度就近似于O(n)。
排序算法优化
各类常见排序算法复杂度比较
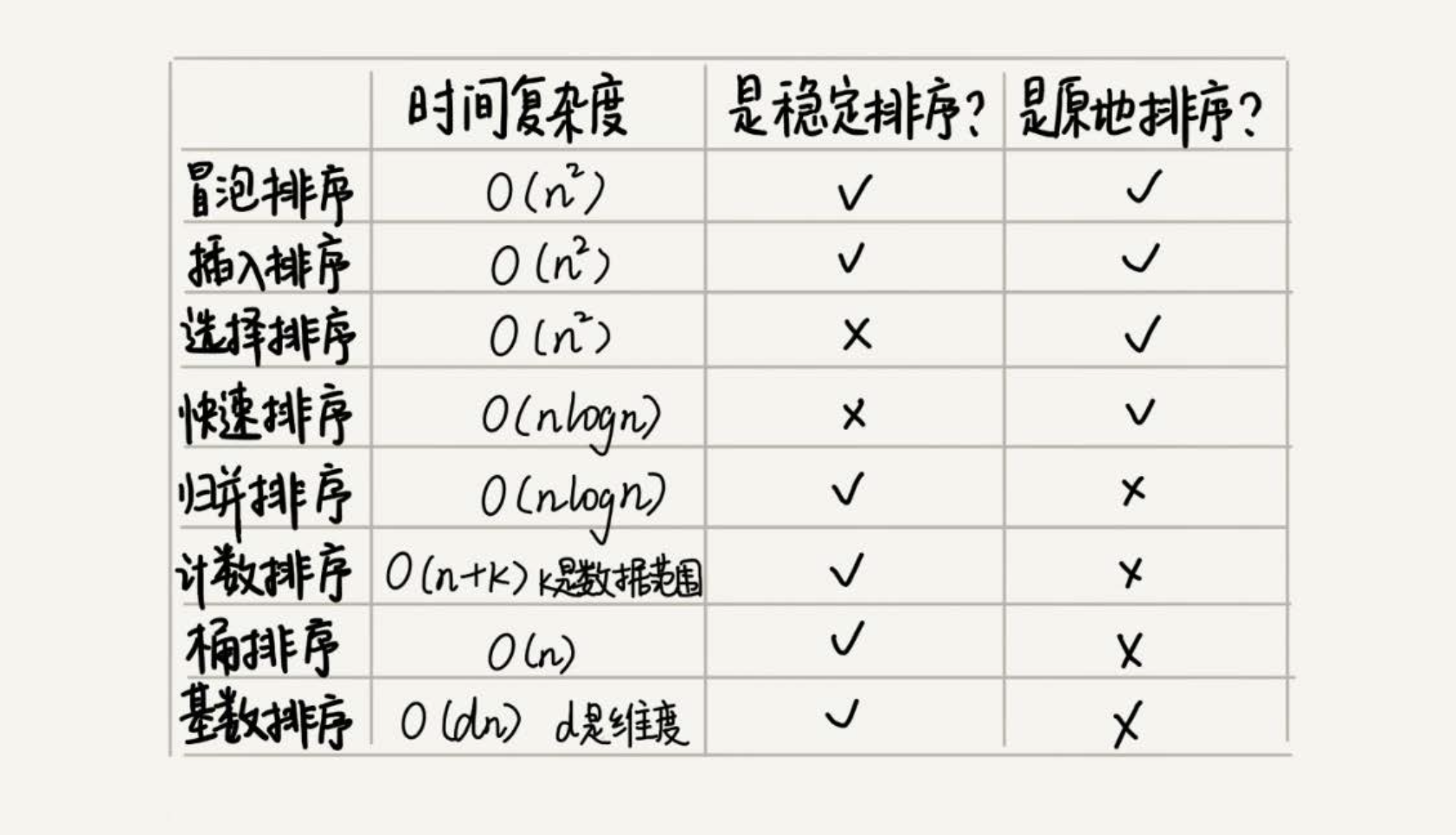
如果对小规模数据进行排序,可以选择时间复杂度是O(n2)的算法;
如果对大规模数据进行排序,时间复杂度是O(nlogn)的算法更加高效。
所以,为了兼顾任意规 模数据的排序,一般都会首选时间复杂度是O(nlogn)的排序算法来实现排序函数。
如何优化快速排序?
快速排序的时间复杂度是O(n2),如果数据原来就是有序的或者接近有序的,每次分区点都选择最后一个数据,
快速排序算法就会变得非常糟糕,时间复杂度就会退化为O(n2)。实际上,这种O(n2)时间复杂度出现的主要原因还是因为我们分区点选的不够合理。
如何选择分区点
最理想的分区点是:被分区点分开的两个分区中,数据的数量差不多。
三数取中法
从区间的首、尾、中间,分别取出一个数,然后对比大小,取这3个数的中间值作为分区点。这样每间隔某个固定的长度,取数据出来比较,将中间值作为分区点的分区算法,肯定要比单纯取某一个数据更好。但是,如果要排序的数组比较大,那“三数取中”可能就不够了,可能要“五数取中”或者“十数取中”。
随机法
随机法就是每次从要排序的区间中,随机选择一个元素作为分区点。这种方法并不能保证每次分区点都选的比较好,但是从概率的角度来看,也不大可能会出现每次分区点都选的很差的情况,所以平均情况下,这样选的分区点是比较好的。时间复杂度退化为最糟糕的O(n2)的情况,出现的可能性不大。
C语言的qsort实现
qsort()会优先使用归并排序来排序输入数据,因为归并排序的空间复杂度是O(n),所以对于小数据量的排序,比如1KB、2KB等, 归并排序只需要额外1KB、2KB的内存空间。
要排序的数据量比较大的时候,qsort()会改为用 快速排序算法来排序。同时qsort()选择分区点的方法是“三数取中法”。
由于递归太深可能会导致堆栈溢出问题,qsort()是通过自己实现一个堆上的栈,手动模拟递归来解决的。
在快速排序的过程中,当要排序的区间中,元素的个数小于等于4时,qsort()就退化为插入排序。

