堆栈与队列

堆栈（Stack）和队列（Queue），这里Stack可以叫做堆栈，也可以叫做栈。但是不能叫做堆，因为堆是Heap，是另外一种数据结构。

Stack

FILO: First In Last Out 先入后出

• Array or Linked List

  最近相关性都可以是用栈解决

Queue

FIFO: First In First Out 先入先出

• Array or Doubly Linked List

Common Data Structure Operations

图片来源 http://www.bigocheatsheet.com/

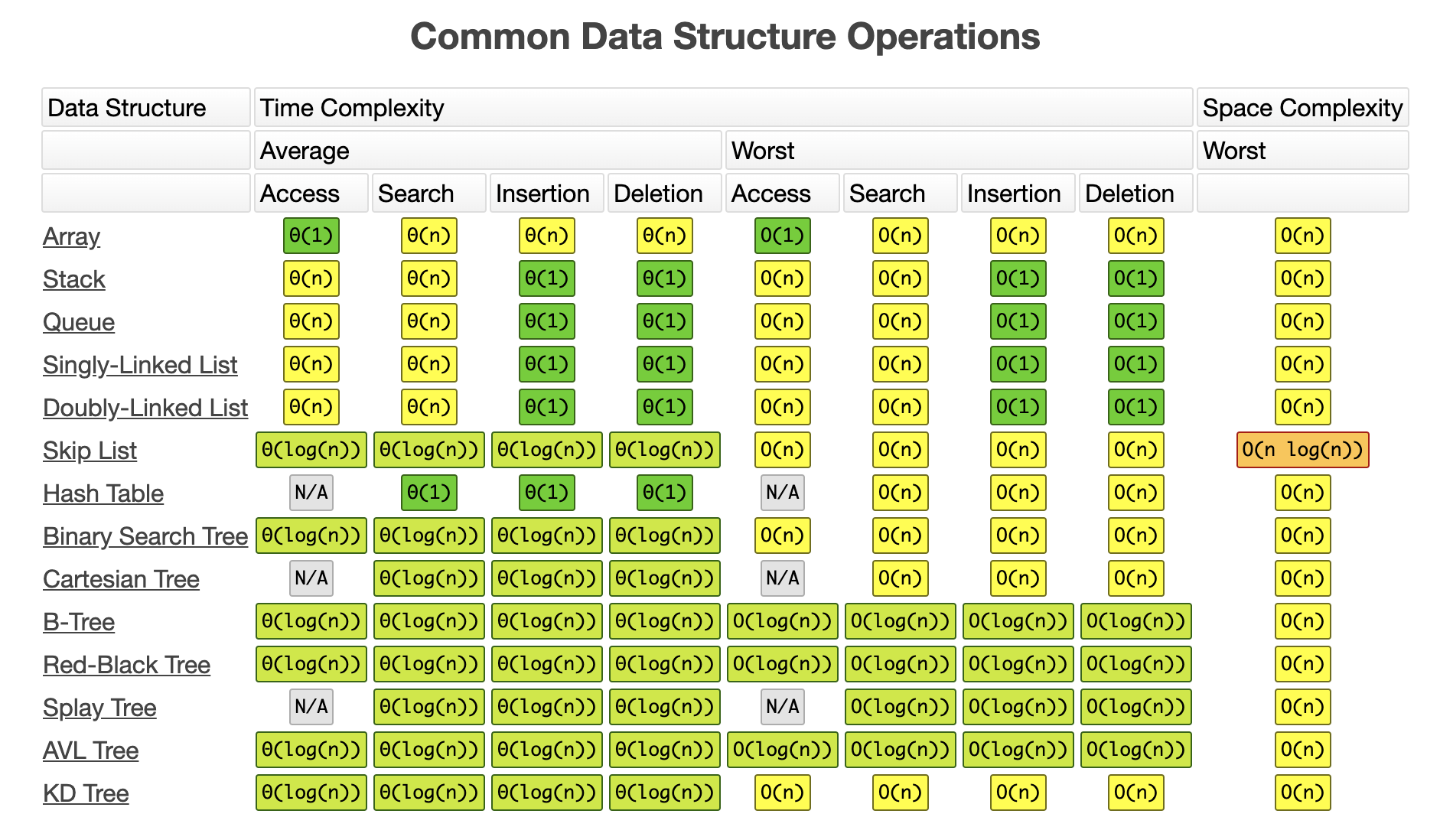
• Time complexity 时间复杂度
• Space Complexity 空间复杂度
• Average 平均
• Worst 最坏
• Access 获取
• Search 搜索
• Insertion 插入
• Deletion 删除部分

有效的括号

给定一个只包括 '('，')'，'{'，'}'，'['，']'的字符串，判断字符串是否有效。

有效字符串需满足：

左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。

示例 1:

输入: "()"
输出: true
示例 2:

输入: "()[]{}"
输出: true
示例 3:

输入: "(]"
输出: false
示例 4:

输入: "([)]"
输出: false
示例 5:

输入: "{[]}"
输出: true

private static Map<Character, Character> baseBracketMap = new HashMap<>();

static {
    // 闭括号作为key，开括号作为value
    baseBracketMap.put(')', '(');
    baseBracketMap.put('}', '{');
    baseBracketMap.put(']', '[');
}

public boolean isValid(String s) {
    Stack<Character> stack = new Stack<>();
    for (int i = 0; i < s.length(); i++) {
        char c = s.charAt(i);
        // 如果是闭括号则进行比较
        if (baseBracketMap.containsKey(c)) {
            char topElement = stack.empty() ? '#' : stack.pop();
            if (topElement != baseBracketMap.get(c)) {
                return false;
            }
        }
        // 开括号则入栈
        else {
            stack.push(c);
        }
    }
    return stack.isEmpty();
}

在学习stack之前，是没有想到太好的使用别的数据结构解决该问题的，但是使用到stack后就可以相对轻松的解决该问题。

1. 开括号需要push到stack中
2. 闭括号要pop出进行匹配是否为对应括号类型
3. 最后匹配完全部元素后，stack需要是空的，否则说明存在没有闭和的开括号

• 代码优化点: Map使用闭括号作为key，方便进行第一次合法比较

复杂度分析

• 时间复杂度：O(n)，因为我们一次只遍历给定的字符串中的一个字符并在栈上进行O(1) 的推入和弹出操作。
• 空间复杂度：O(n)，当我们将所有的开括号都推到栈上时以及在最糟糕的情况下，我们最终要把所有括号推到栈上。例如 ((((((((((

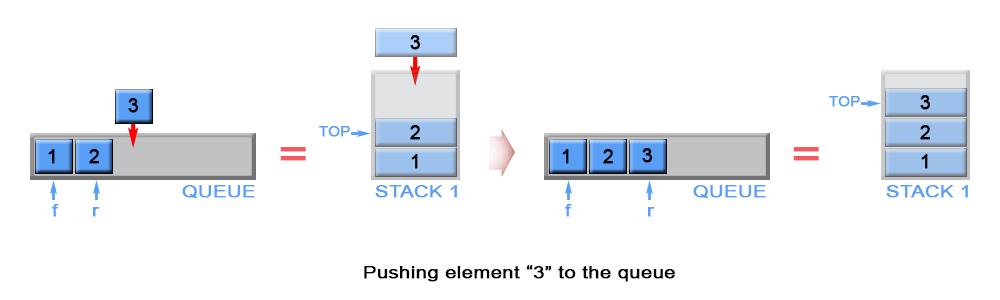
用栈实现队列

使用栈实现队列的下列操作：

push(x) -- 将一个元素放入队列的尾部。
pop() -- 从队列首部移除元素。
peek() -- 返回队列首部的元素。
empty() -- 返回队列是否为空。

示例:

MyQueue queue = new MyQueue();

queue.push(1);
queue.push(2);  
queue.peek();  // 返回 1
queue.pop();   // 返回 1
queue.empty(); // 返回 false

说明:
你只能使用标准的栈操作 -- 也就是只有 push to top, peek/pop from top, size, 和 is empty 操作是合法的。
你所使用的语言也许不支持栈。你可以使用 list 或者 deque（双端队列）来模拟一个栈，只要是标准的栈操作即可。
假设所有操作都是有效的 （例如，一个空的队列不会调用 pop 或者 peek 操作）。

双栈处理

主要的思路是通过双栈的数据结构，通过不断pop和push的操作来调换位置。

入队 - O(n)， 出队 - O(1)，在push的时候做文章

pop、peek还是通过s1直接进行操作，但在push的时候，通过两个栈对数据位置进行调换

class MyQueue2 {
    private Stack<Integer> s1 = new Stack<Integer>();
    private Stack<Integer> s2 = new Stack<Integer>();
    private Integer front;

    public MyQueue2() {
    }

    public void push(int x) {
        if (s1.empty()) {
            front = x;
        }
        while (!s1.isEmpty()) {
            s2.push(s1.pop());
        }
        s2.push(x);
        while (!s2.isEmpty()) {
            s1.push(s2.pop());
        }

    }

    public int pop() {
        int i = s1.pop();
        if (!s1.empty()) {
            front = s1.peek();
        }
        return i;
    }

    public int peek() {
        return front;
    }

    public boolean empty() {
        return s1.isEmpty();
    }
}

复杂度分析

入队

• 时间复杂度：O(n): 对于除了新元素之外的所有元素，它们都会被压入两次，弹出两次。新元素只被压入一次，弹出一次。这个过程产生了 4n + 2 次操作，其中n是队列的大小。由于 压入 操作和 弹出 操作的时间复杂度为 O(1)， 所以时间复杂度为 O(n)。
• 空间复杂度：O(n): 需要额外的内存来存储队列中的元素。

出队、判空

• 时间复杂度：O(1)
• 空间复杂度：O(1)

入队 - O(1)，出队 - 摊还复杂度 O(1)，在pop的时候做文章

新元素总是压入 s1 的栈顶，同时我们会把 s1 中压入的第一个元素赋值给作为队首元素的 front 变量。

根据栈 LIFO 的特性，s1 中第一个压入的元素在栈底。为了弹出 s1 的栈底元素，我们得把 s1 中所有的元素全部弹出，再把它们压入到另一个栈 s2 中，这个操作会让元素的入栈顺序反转过来。通过这样的方式，s1 中栈底元素就变成了 s2 的栈顶元素，这样就可以直接从 s2 将它弹出了。一旦 s2 变空了，我们只需把 s1 中的元素再一次转移到 s2 就可以了。&oq=根据栈 LIFO 的特性，s1 中第一个压入的元素在栈底。为了弹出 s1 的栈底元素，我们得把 s1 中所有的元素全部弹出，再把它们压入到另一个栈 s2 中，这个操作会让元素的入栈顺序反转过来。通过这样的方式，s1 中栈底元素就变成了 s2 的栈顶元素，这样就可以直接从 s2 将它弹出了。一旦 s2 变空了，我们只需把 s1 中的元素再一次转移到 s2 就可以了。

极客时间中覃超讲解该题也是用的这个方法，简单理解就是两个Input栈、Output栈。push都放到Input，pop从Output出。如果output为空，则从input逐个pop到input中（顺序正好会调转）。

class MyQueue3 {
    private Stack<Integer> s1 = new Stack<Integer>();
    private Stack<Integer> s2 = new Stack<Integer>();
    private Integer front;

    public MyQueue3() {
    }

    public void push(int x) {
        if (s1.empty()) {
            front = x;
        }
        s1.push(x);
    }

    public int pop() {
        if (s2.isEmpty()) {
            while (!s1.isEmpty()) {
                s2.push(s1.pop());
            }
        }
        return s2.pop();
    }

    public int peek() {
        if (!s2.isEmpty()) {
            return s2.peek();
        }
        return front;
    }

    public boolean empty() {
        return s1.isEmpty() && s2.isEmpty();
    }
}

复杂度分析

入队

• 时间复杂度：O(1) 向栈压入元素的时间复杂度为O(1)
• 空间复杂度：O(n) 需要额外的内存来存储队列元素

出队

• 时间复杂度： 摊还复杂度 O(1)，最坏情况下的时间复杂度 O(n)
  在最坏情况下，s2 为空，算法需要从 s1 中弹出 n 个元素，然后再把这 n 个元素压入 s2，在这里nn代表队列的大小。这个过程产生了 2n 步操作，时间复杂度为 O(n)。但当 s2 非空时，算法就只有 O(1) 的时间复杂度。所以为什么叫做摊还复杂度O(1) 呢？ 读了下一章你就知道了。
• 空间复杂度 ：O(1)

使用队列实现栈

使用队列实现栈的下列操作：

push(x) -- 元素 x 入栈
pop() -- 移除栈顶元素
top() -- 获取栈顶元素
empty() -- 返回栈是否为空

注意:
你只能使用队列的基本操作-- 也就是 push to back, peek/pop from front, size, 和 is empty 这些操作是合法的。
你所使用的语言也许不支持队列。 你可以使用 list 或者 deque（双端队列）来模拟一个队列 , 只要是标准的队列操作即可。
你可以假设所有操作都是有效的（例如, 对一个空的栈不会调用 pop 或者 top 操作）。

双队列 压入 -O(1)， 弹出 -O(n)

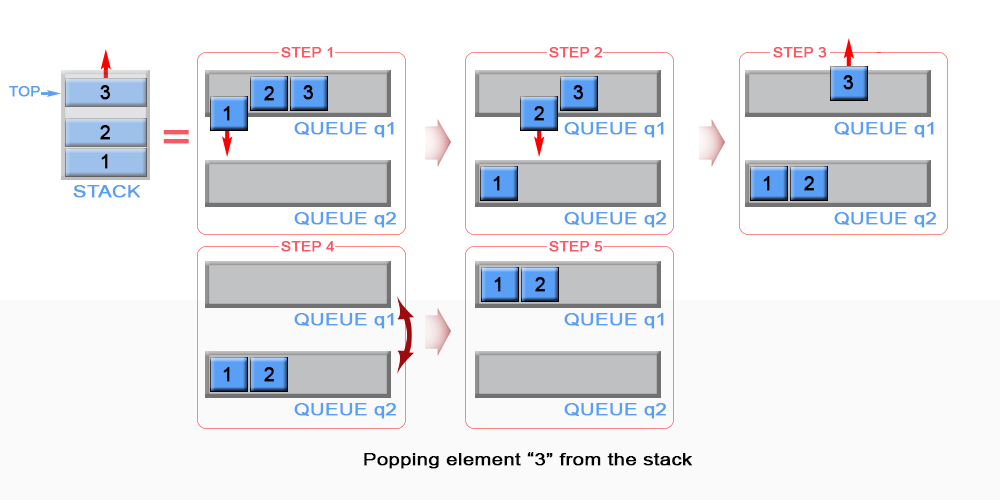
双队列 压入 -O(n)， 弹出 -O(1)

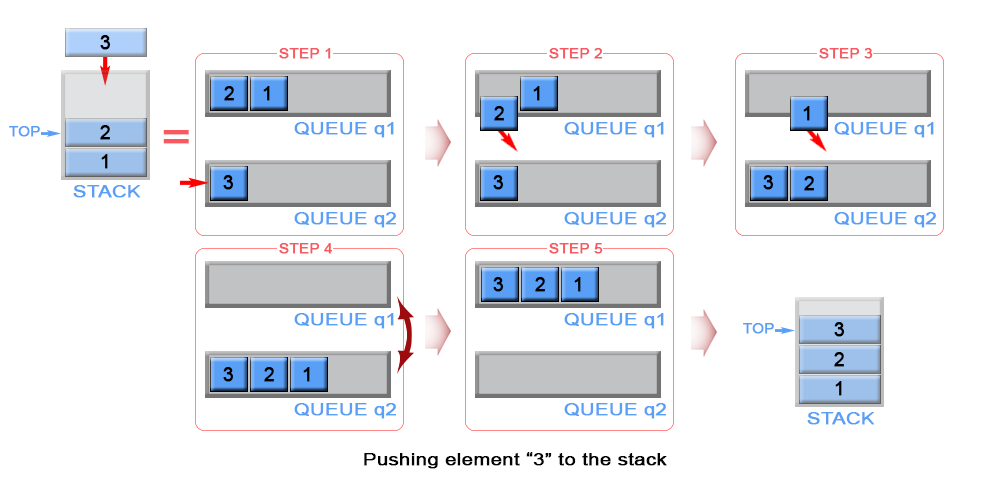
列出其中一种pop的时候做处理，push、top的时候从第一个队列中直接取

public class MyStack {

    private Queue<Integer> q1 = new LinkedList();
    private Queue<Integer> q2 = new LinkedList();

    private int top;

    public MyStack() {
    }

    public void push(int x) {
        q1.add(x);
        top = x;
    }

    public int pop() {
        while (q1.size() > 1) {
            top = q1.remove();
            q2.add(top);
        }
        int i = q1.remove();
        Queue<Integer> temp = q1;
        q1 = q2;
        q2 = temp;
        return i;
    }

    public int top() {
        return top;
    }

    public boolean empty() {
        return q1.isEmpty();
    }
}

PriorityQueue 优先队列

正常入，按照优先级出。优先级是优先队列本身的一个属性，可以是最大的先出、最小的先出，或者是设置每个元素出现的次数等等。

• 插入操作: O(1)
• 取出操作: O(logN) 按照元素的优先级取出

实现机制

• Heap
  • Binary 二叉堆
  • Binomial 多项式堆
  • Fibonacci 斐波那契堆
• Binary Search Tree 二叉搜索树

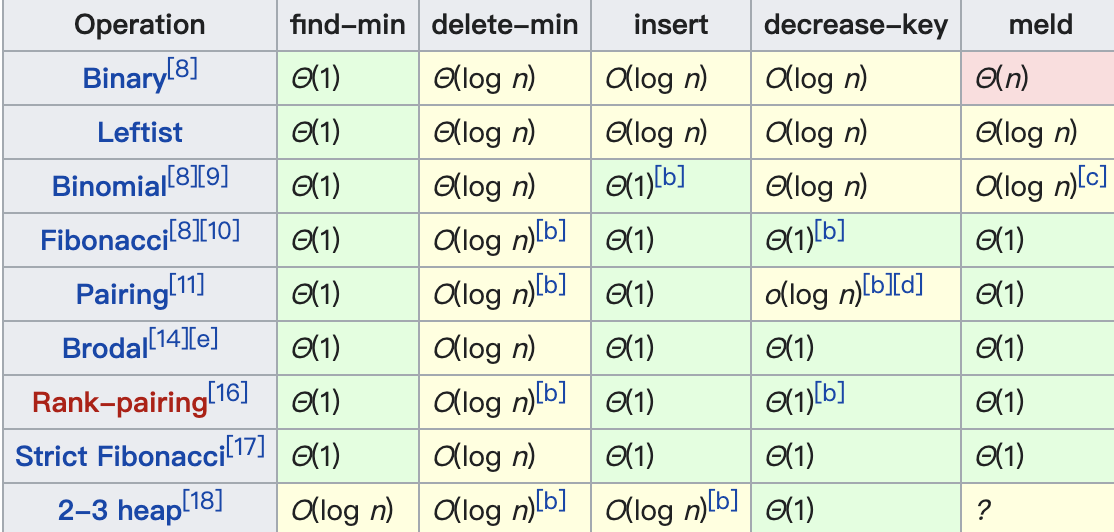
各类堆的操作时间复杂度