数组(Array)与链表(LinkedList)都是比较基础的线性数据结构,基础概念就不记录了,主要记录一些算法题和解题思路。题目全部来源于LeetCode,部分解析内容直接参考了具体LeetCode题中高赞评论
SkipList跳表
跳表在学习Redis的Redis Object的Encoding的时候已经有了解过了,主要记录下该数据结构的思想,运用到的是一个数据结构和算法的常用方法:升唯,空间换时间
复杂度分析
现实当中使用跳表的时候,会由于跳表元素的增加删除等操作,导致索引步数量并不一致,有的可能跨两个元素,有可能会更多。增加、删除的维护成本更高,时间复杂度为logn。
查询时间复杂度分析
n/2、n/4、n/8、第K级索引结点的个数就是n/(2^k),假设索引有h级,最高级的索引有2个结点。n/(2^h) = 2,从而求得h = log2(n)-1
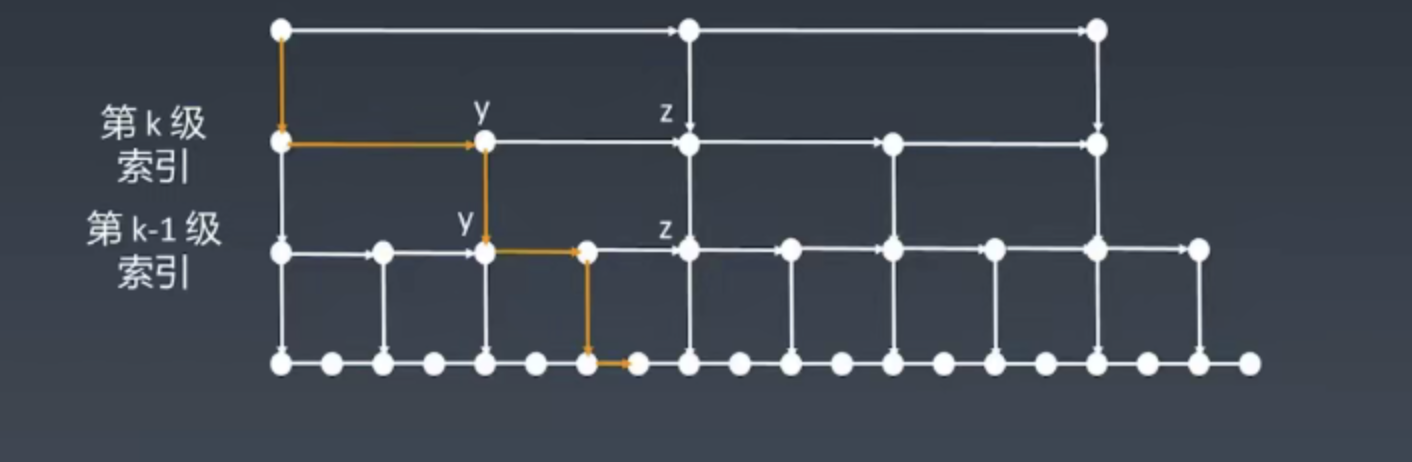
- 索引的高度:logn,每层索引遍历的结点个数:3
- 在跳表中查询任意数据的时间复杂度就是O(logn)
空间复杂度分析
原始链表大小为n,每2个结点抽1个,每层索引的结点数为:n/2、n/4、n/8 … 8,4,2
原始链表大小为n,每3个结点抽1个,每层索引的结点数为:n/3、n/3、n/27 … 9,3,1
- 空间复杂度是O(n)
是比原始的链表空间复杂度多一些,就是上面几层的索引,只不过每一层都是除以二。
相关链接
LRU Cache - Linked List
Redis - Skip List
- https://redisbook.readthedocs.io/en/latest/internal-datastruct/skiplist.html
- https://www.zhihu.com/question/20202931
搜索插入位置
1 | 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 |
心得
在评级中是简单的一道题。其实还挺微妙的。直观的解决办法就是遍历,同时判断是否超过当前元素。但这样相当于暴力处理,时间复杂度是O(n)。首先给定的是一个有序数组,好在以前了解过二分查找,所以可以采用二分查找的方式。
因为是用java写的,当时发现了一个要注意的事情,就是右移低于加法的运算优先级。还有一点就是求mid,一般是用(left + right) >> 2,但其实并不严谨,因为可能会出现整型超出范围的问题。所以可以修改为((right - left) >> 1) + left。除此之外询问了朋友,可能会出现两个中位数和死循环的情况,但还没学到具体的场景,之后会在补充。
二分查找解法
1 | public int searchInsert(int[] nums, int target) { |
反转一个单链表
1 | 示例: |
使用外部容器
将链表中的元素依次放入外部容器中,如ArrayList,使用容器本身提供的反转能力进行反转。不过这样的处理方式占用空间会加大。
双指针迭代
1 | public ListNode reverseList(ListNode head) { |
- 时间复杂度:O(n),假设n是列表的长度,时间复杂度是O(n)
- 空间复杂度:O(1)
是一种很直观的解决方式,遍历当前节点。分别记录前驱节点和当前节点,并且取出当前节点的后序节点指向当前节点进行下一次遍历,直到当前节点为空的时候,则反转结束
递归
1 | public ListNode reverseList(ListNode head) { |
- 终止条件是当前节点或者下一个节点==null
在函数内部,改变节点的指向,也就是head的下一个节点指向head递归函数那句1
head.next.next = head
老实说递归的解法想了半天没想出来,看到别人的解也是比较懵,不知道如何理解。建议看下该评论中的幻灯片比较容易理解。
其实就是head的下一个节点指向head。递归函数中每次返回的cur其实只最后一个节点,在递归函数内部,改变的是当前节点的指向。
两两交换链表中的节点
1 | 给定一个链表,两两交换其中相邻的节点,并返回交换后的链表。 |
- 本题的递归和非递归解法其实原理类似,都是更新每两个点的链表形态完成整个链表的调整
- 其中递归解法可以作为典型的递归解决思路进行讲解
- 递归写法要观察本级递归的解决过程,形成抽象模型,因为递归本质就是不断重复相同的事情。而不是去思考完整的调用栈,一级又一级,无从下手。如图所示,我们应该关注一级调用小单元的情况,也就是单个f(x)。
其中我们应该关心的主要有三点:
- 返回值
- 调用单元做了什么
- 终止条件
在本题中:
- 返回值:交换完成的子链表
- 调用单元:设需要交换的两个点为 head 和 next,head 连接后面交换完成的子链表,next 连接 head,完成交换
- 终止条件:head 为空指针或者 next 为空指针,也就是当前无节点或者只有一个节点,无法进行交换
递归解法
1 | class Solution { |
非递归解法
1 | class Solution { |
环形链表
1 | 给定一个链表,判断链表中是否有环。 |
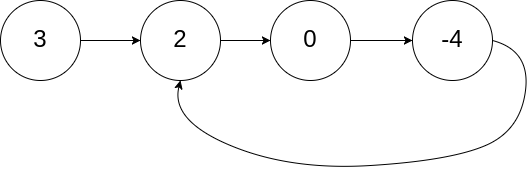
1 | 示例 2: |
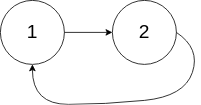
1 | 示例 3: |

哈希表
1 | public static boolean hasCycle(ListNode head) { |
主要就是用哈希表来存储被访问过的节点,如果节点已经被访问过了,则相当于链表中有环。
复杂度分析
- 时间复杂度:O(n),对于含有n个元素的链表,我们访问每个元素最多一次。添加一个结点到哈希表中只需要花费 O(1)的时间。
- 空间复杂度:O(n),空间取决于添加到哈希表中的元素数目,最多可以添加n个元素。
双指针
后面看了别人的解题学习到的解决方式,提供了另外一种解决思路。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16public static boolean hasCycleDoublePointer(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode slow = head;
ListNode fast = head.next;
while (slow != fast) {
// 如果快指针已经到达重点,则链表无环
if (fast == null || fast.next == null) {
return false;
}
slow = slow.next;
fast = fast.next.next;
}
return true;
}
主要的思路是,设置两个指针,一个是慢指针,每次移动1位。另一个是快指针,每次移动2位。那么如果快指针到达重点。则说明没有环。如果没有到达重点。快指针必定会追上慢指针相遇。
复杂度分析
时间复杂度:O(n),让我们将n设为链表中结点的总数。为了分析时间复杂度,我们分别考虑下面两种情况。
- 链表中不存在环:快指针将会首先到达尾部,其时间取决于列表的长度,也就是O(n)。
链表中存在环:我们将慢指针的移动过程划分为两个阶段:非环部分与环形部分:
- 慢指针在走完非环部分阶段后将进入环形部分:此时,快指针已经进入环中
迭代次数=非环部分长度=N - 两个指针都在环形区域中:考虑两个在环形赛道上的运动员 - 快跑者每次移动两步而慢跑者每次只移动一步。其速度的差值为 1,因此需要经过
二者之间距离/速度差值次循环后,快跑者可以追上慢跑者。这个距离几乎就是 “环形部分长度 K” 且速度差值为 1,我们得出这样的结论迭代次数=近似于"环形部分长度 K
因此,在最糟糕的情形下,时间复杂度为
O(N+K),也就是O(n)。- 慢指针在走完非环部分阶段后将进入环形部分:此时,快指针已经进入环中
空间复杂度:O(1),只使用了慢指针和快指针两个结点,所以空间复杂度为O(1)。
双指针变种(会破坏链表结构)
在leetcode评论区看到的,一种会破坏链表结构的解法。不过结果是对的。
思路是不断的将自己与下下个进行对比,最终如果自己指向了自己 即head == head.next则说明出现了环。没有则说明无环。虽然会破坏链表结构,不过就题目而言也是一种解法。1
2
3
4
5
6
7
8
9
10
11
12public static boolean hasCycleBreak(ListNode head) {
while (head != null) {
if (head == head.next) {
return true;
}
if (head.next != null) {
head.next = head.next.next;
}
head = head.next;
}
return false;
}
环形链表 II
1 | 给定一个链表,返回链表开始入环的第一个节点。 如果链表无环,则返回 null。 |
该题和上一道是非常接近的问题,如果采用外部容器如哈希表,就会很容易解出。但难点在于如何不使用外部容器解决。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36/**
* 返回环的交汇点 即双指针交汇点
* @param head
* @return
*/
private ListNode getIntersect(ListNode head) {
ListNode slow = head;
ListNode fast = head;
while (fast != null && fast.next != null) {
slow = slow.next;
fast = fast.next.next;
if (slow == fast) {
return slow;
}
}
return null;
}
public ListNode detectCycle(ListNode head) {
if (head == null) {
return null;
}
// 获取交汇点
ListNode intersect = getIntersect(head);
if (intersect == null) {
return null;
}
// 双指针分别从头、交汇点同步长出发。再次交汇点即入环点
ListNode ptr1 = head;
ListNode ptr2 = intersect;
while (ptr1 != ptr2) {
ptr1 = ptr1.next;
ptr2 = ptr2.next;
}
return ptr1;
}
本题获取交汇点后,分别从头、交汇点同步长出发。再次交汇点即是入环点。
这个有一个数学的推导过程,感兴趣可以看下该题官方答案的解析,或者参考这个我一个朋友自己做的笔记,我当时是没有理解这个推导过程的,但是看了他的笔记后就大概明白了。
K 个一组翻转链表
1 | 给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。 |
盛最多水的容器
1 | 给你 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。 |
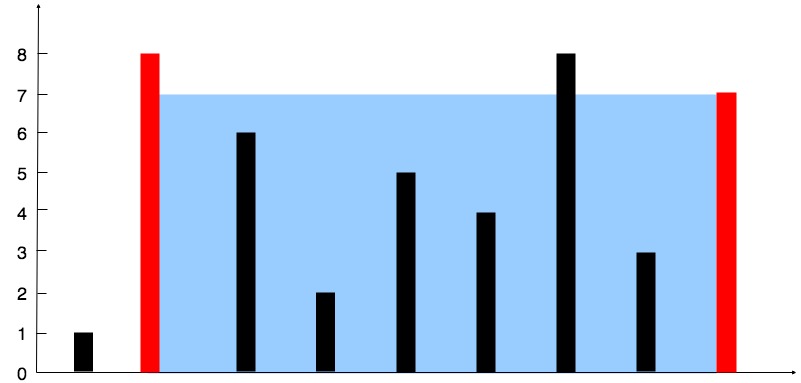
抽象问题为数学模型
人脑思考的最简单的方法。枚举全部的元素,left bar x,right bar y,(x-y)* hight_diff
两层for循环迭代
两层for遍历获取x和y,计算长度和最大(最高)的值相乘,但是由于是两层for循环遍历,所以时间复杂度是O(n^2)1
2
3
4
5
6
7
8
9
10public int maxArea(int[] height) {
int max = 0;
for (int i = 0; i < height.length - 1; i++) {
for (int j = i + 1; j < height.length; j++) {
int area = (j - i) * Math.min(height[i], height[j]);
max = Math.max(area, max);
}
}
return max;
}
双指针
最初我们可以复用上面的逻辑,进行双指针的迭代,再进行计算面积,这样时间复杂度就是O(n)
但是我们可以抽象出问题,可以从两端边界向内收敛计算面积比较。i往右边走,j往左边走,哪个小则向内侧移动。是一种非常常见的解决问题的思路1
2
3
4
5
6
7
8public int maxArea_2(int[] height) {
int max = 0;
for (int i = 0, j = height.length - 1; i < j; ) {
int minHeight = height[i] < height[j] ? height[i++] : height[j--];
max = Math.max(max, (j - i + 1) * minHeight);
}
return max;
}

